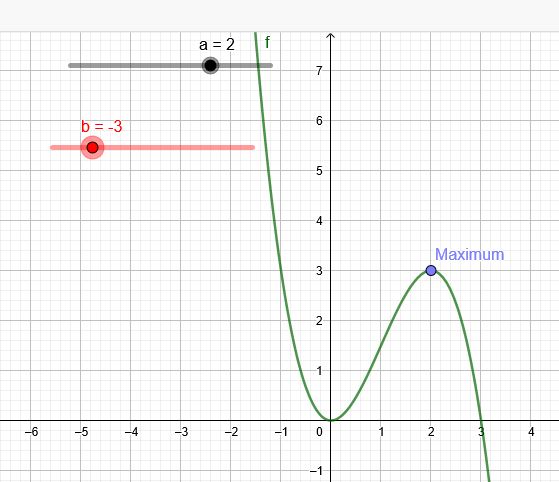
Wie erhält man eine Formel für die folgende Kurve zwischen Punkt A und Punkt B.
Dabei ist Punkt A als ein Minima bei M\((0|0)\) fest und Punkt B sei mit B\((a | b)\) variabel und sollte ein Maxima sein. (3.Grad)
\(f(x)=ex^2(x-N)\)
B\((a | b)\):
\(f(a)=e\cdot a^2(a-N)=e(a^3-a^2\cdot N)=b\)
\(e=\frac{b}{a^3-a^2\cdot N}\)
\(f(x)=\frac{b}{a^3-a^2\cdot N}[x^3-Nx^2]\)
\(f'(x)=\frac{b}{a^3-a^2\cdot N}[3x^2-2Nx]\)
\(f'(a)=\frac{b}{a^3-a^2\cdot N}[3a^2-2aN]\)
\(\frac{b}{a^3-a^2\cdot N}[3a^2-2aN]=0\)
\(3a^2-2aN=0\) \(N=1,5a\) \(e=\frac{b}{a^3-a^2\cdot 1,5a}=\frac{b}{a^3-1,5a^3}=\frac{b}{0,5a^3}\)
\(f(x)=\frac{2b}{a^3}\cdot x^2(x-1,5a)=\frac{2b}{a^3}\cdot (x^3-1,5a x^2)\)
\(f'(x)=\frac{2b}{a^3}\cdot (3x^2-3a x)\)
\(\frac{2b}{a^3}\cdot (3x^2-3a x)=0\)
\(x_1=0\)
\(x_2=a\)
\(f''(x)=\frac{2b}{a^3}\cdot (6x-3a )\)
\(f''(a)=\frac{2b}{a^3}\cdot (3a )=\frac{6b }{a^2}\)
Für ein Maximum bei B muss gelten \(\frac{6b }{a^2}<0\) → \(b <0\)