Ableitung gesucht Funktion

Question

Aufgabe:

Gegeben ist die Funktion

\( f(x)=5 x^{2} \cdot e^{\left(8 x^{7}+3 x\right)} \)

Gesucht ist die erste Ableitung f′(x) an der Stelle =−0.63

Problem/Ansatz:

Hab als Ergebnis 3,07147 rausbekommen. Stimmt das?

Comments

Wer stellt denn derartig bekloppte Aufgaben?

---

ja ist richtig blöd

---

Zur Kontrolle : 0.728

---

Vom Duplikat:

Titel: Ableitung + eulersche Zahl

Stichworte: eulersche-zahl,wirtschaftsmathematik,funktion,ableitungen,ableiten

Aufgabe:

Gegeben ist die Funktion

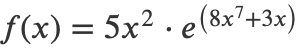
Gesucht ist die erste Ableitung f′(x) an der Stelle =−0.63.

Problem/Ansatz:

Habe Die Ableitung berechnet und -0.63 für x eingesetzt. Es kommt 0.73 gerundet heraus. Stimmt das?

---

Die Antwort auf diese Frage hatte dir bereits Tschakabumba gegeben.

Answer 1

Aloha :)

Hier helfen die Produkt und die Kettenregel weiter:$$f(x)=\underbrace{5x^2}_{=u}\cdot \underbrace{e^{8x^7+3x}}_{=v}\quad\implies$$$$f'(x)=\overbrace{10x}^{=u'}\cdot \overbrace{e^{8x^7+3x}}^{=v}+\overbrace{5x^2}^{=u}\cdot\overbrace{\underbrace{e^{8x^7+3x}}_{=\text{äußere Abl.}}\cdot\underbrace{(8x^7+3x)'}_{=\text{innere Abl.}}}^{=v'}$$$$\phantom{f'(x)}=10x\cdot e^{8x^7+3x}+5x^2\cdot e^{8x^7+3x}\cdot(56x^6+3)=e^{8x^7+3x}\left(10x+5x^2(56x^6+3)\right)$$$$\phantom{f'(x)}=e^{8x^7+3x}\cdot5x\left(2+56x^7+3x\right)$$

Comments

danke dir:) also kommt raus -0.80 richtig?

---

Da hast du dich beim Einsetzen vermutlich vertippt. Ich bekomme:$$f'(-0,63)\approx0,727773$$

---

dankeschönn!!! für die Hilfe:)

Answer 2

Das Ergebnis stimmt nicht.

Comments

Könntest du mir dann bitte weiterhelfen?

---

Überlege um welche Art von Term es sich handelt. Zur Auswahl stehen

• Summe/Differenz
• Produkt
• Quotient
• Potenz
  
• Funktionsanwendung
  
• Funktionsverkettung

Bestimme die Ableitungsfunktion indem du die zur Art des Terms passende Ableitungsregel anwendest.

Setze -0.63 in die Ableitungsfunktion ein.

Answer 3

Ja.

Ein anderer Benutzer hat es Dir übrigens gestern hier vorgerechnet.

Answer 4

f '(x) = 10x*e^(8x^7+3x^2) +5x^2*e^(8x^7+3x)*(56x^6+3)

= 5x*e^(8x^7+3x)*( 2+56x^7+3x)

f'(-0,63) = 0,73

Dein Ergebnis stimmt. :)