Limes gebrochen rationaler Funktionen

Question

Aufgabe:

Problem/Ansatz:

wenn ich die Funktion 1-x²/2x-1 habe.

Und ich limes also das unendlichkeitsverhalten bestimme.

Wie mache ich das?


Ich hatte geschrieben
Lim x-> +0,71 von links = positiv unendlich.

Meine Lehrerin meinte aber das ist falsch.

Answer 1

Bitte Funktion richtig abschreiben. Es fehlen Klammern.

Comments

f(x) = (1-x²)/(2x²-1)

---

f(x) = (1-x²)/(2x-1)

Okay, und welchen Limes suchst Du? Gegen unendlich, gegen negativ unendlich, gegen 1/2, links- oder rechtsseitig?

Und woher hast Du 0,71?

---

Gegen 0.71 linksseitig :)

---

Gegen 0.71 linksseitig

Da braucht es keinen Grenzwert. Setze einfach 0,71 in die Funktion ein.

---

Das hab ich gemacht. Aber ich komm anstatt auf minus unendlich auf plus unendlich

---

Wenn man x = 0,71 in die Funktion einsetzt, ist das Ergebnis \( \frac{1653}{1400} \) = 1,18...

---

Das ist die Funktion:

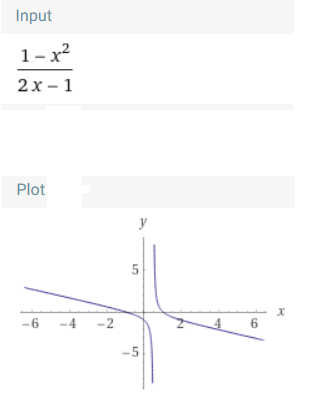
Mögliche Grenzwerte sind:

\(\lim \limits_{x \rightarrow-\infty} \frac{1-x^{2}}{2 x-1}=+\infty\)

\(\lim \limits_{x \rightarrow \infty} \frac{1-x^{2}}{2 x-1}=-\infty\)

\(\lim \limits_{x \uparrow\frac{1}{2}} \frac{1-x^{2}}{2 x-1}=-\infty\)

\(\lim \limits_{x \downarrow\frac{1}{2}} \frac{1-x^{2}}{2 x-1}=+\infty\)

---

Achso ok vielen vielen lieben dank . Und wie wäre es bei der Funktion

f(x)= (1-x²)/(2x²-1)

---

Du hast immer noch nicht gesagt, woher Du 0,71 hast.

---

Die funktion f(x)= (1-x²)/(2x²-1)

Ist ausklammern f(x)= ((x-1)*(x+1))/(2*(x- Wurzel 2/2)*(x+Wurzel2/2)

---

Und wurzel2/2 ist gerundet 0.71

---

Achso, Du hast nun noch ein Quadrat hergezaubert.

Da sind die Polstellen aber nicht bei 0,71 sondern bei \(± \frac{1}{\sqrt{2}} \) was nicht exakt dasselbe ist.

Hast Du diese neue Funktion mal geplottet?

---

Hallo Fragesteller,

von welcher Funktion sprichst du denn die ganze Zeit ?
Hier scheint es zwei verschiedene Versionen zu geben !!

---

Der Fragesteller hat wohl zuerst die Klammern vergessen, und später noch ein Quadrat hineingeflickt.

---

Von der Funktion (1-x²)/(2x²-1)

---

Ich hab es herausgefunden. Trotzdem danke für die mühe

Answer 2

Wenn du meinst:

(1-x^2)/(2x-1) , dann gilt:

Kürzen mit x^2;

(1/x^2-1)/(2/x-1/x^2) = (0-1)/(0-0) = -oo für x gegen oo

oder kurz:

Der Zähler wächst schneller als der Nenner. -x^2 entscheidet und das geht gegen -oo, wenn x gegen +- oo geht.

Was hast du gerechnet?

Answer 3

f ( x ) = ( 1 - x^2) / ( 2x-1 ) | * -1 / -1
f ( x ) = ( x^2- 1 ) / ( -2x +1 ) |
bei x -> ∞ entfällt die eins, spielt
für das Ergebnis keine Rolle mehr
bei x -> ∞ [ x^2 / ( -2x ) ] = [ - x ] oder - ∞
bei x -> -∞ [ x^2 / ( -2x ) ] = [ - x ] oder + ∞

Polstelle
f ( x ) = ( 1 - x^2) / ( 2x-1 )
Division durch 0 nicht definert
2x - 1 =

x = 1/2

Jetzt den links- bzw rechtsseitigen Grenzwert
bestimmen.

Comments

Jetzt den links- bzw rechtsseitigen Grenzwert
bestimmen.

Genau das war ja des Fragestellers Problem :)

Allerdings für eine andere Funktion (er hat sie erst später korrigiert).

---

( 1 - x^2) / ( 2x-1 )
linkseitig ( Nenner )
lim x -> 1/2 (-) [ 2x-1 ] = 1 (-) - 1
0.9999... - 1 = - 0.00001
Zusammen ( ( 1- 1/2 ^2 ) = 3/4
3/4 / - 0.0001 = - ∞

---

Er will es für eine andere Funktion :)

Aber oben hat er ja geschrieben, dass er es mittlerweile selber gefunden hat.