Aloha :)
Willkommen in der Mathelounge... \o/
\(|x|\) und \(|x-1|\) liegen sehr nahe beieinander, das ist verdächtig. Wir schauen da mal genauer hin:$$x\le0\implies|x|=-x\text{ und }|x-1|=-(x-1)=1-x$$$$\phantom{x\le0}\implies|x|-|x-1|=-x-(1-x)=-1$$$$x\ge1\implies|x|=x\text{ und }|x-1|=x-1$$$$\phantom{x\le0}\implies|x|-|x-1|=x-(x-1)=1$$$$x\in(0;1)\implies |x|=x\text{ und }|x-1|=-(x-1)=1-x$$$$\phantom{x\in(0;1)}\implies |x|-|x-1|=x-(1-x)=2x-1$$Das hat sich doch gelohnt, wir fassen mal zusammen:
$$|x|-|x-1|+|y|>3\Longleftrightarrow\left\{\begin{array}{ll}-1+|y|>3 &\text{falls }x\le0\\2x-1+|y|>3 & \text{falls }0<x<1\\1+|y|>3 &\text{falls }x\ge1\end{array}\right.$$$$|x|-|x-1|+|y|>3\Longleftrightarrow\left\{\begin{array}{ll}|y|>4 &\text{falls }x\le0\\|y|>4-2x & \text{falls }0<x<1\\|y|>2 &\text{falls }x\ge1\end{array}\right.$$$$|x|-|x-1|+|y|>3\Longleftrightarrow\left\{\begin{array}{ll}y<-4\;\lor y>4 &\text{falls }x\le0\\y<2x-4\;\lor\;y>4-2x & \text{falls }0<x<1\\y<-2\;\lor\;y>2 &\text{falls }x\ge1\end{array}\right.$$
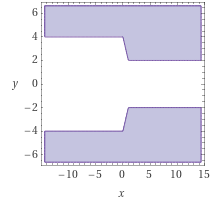
Das solltest du nun skizzieren können.