Eigenwerte, Eigenvektoren bestimmen

Question

Aufgabe:

Hallo!

Ich komm wieder mit dem Zusammenfassen nicht klar. Am Ende ist es sinnvoll, die Werte richtig zusammenzufassen, aber ich hab da noch große Schwierigkeiten. Könnt ihr mir da weiterhelfen Text erkannt:

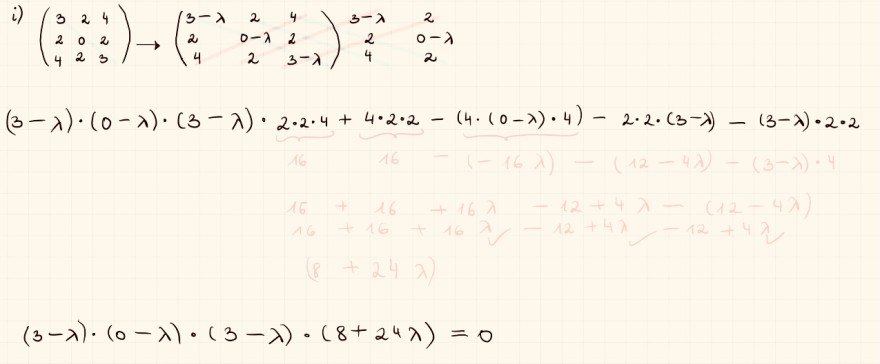
Text erkannt:

i) \( \left(\begin{array}{lll}3 & 2 & 4 \\ 2 & 0 & 2 \\ 4 & 2 & 3\end{array}\right) \rightarrow\left(\begin{array}{ccc}3-\lambda & 2 & 4 \\ 2 & 0-\lambda & 2 \\ 4 & 2 & 3-\lambda\end{array}\right) \begin{array}{cc}3-\lambda & 2 \\ 2 & 0-\lambda \\ 4 & 2\end{array} \) \( (3-\lambda) \cdot(0-\lambda) \cdot(3-\lambda) \cdot 2 \cdot 2 \cdot 4+4 \cdot 2 \cdot 2-(4 \cdot(0-\lambda) \cdot 4)-2 \cdot 2 \cdot(3-\lambda)-(3-\lambda) \cdot 2 \cdot 2 \) \( (3-\lambda) \cdot(0-\lambda) \cdot(3-\lambda) \cdot(8+24 \lambda)=0 \)

i) \( \left(\begin{array}{lll}3 & 2 & 4 \\ 2 & 0 & 2 \\ 4 & 2 & 3\end{array}\right) \rightarrow\left(\begin{array}{ccc}3-\lambda & 2 & 4 \\ 2 & 0-\lambda & 2 \\ 4 & 2 & 3-\lambda\end{array}\right) \begin{array}{cc}3-\lambda & 2 \\ 2 & 0-\lambda \\ 4 & 2\end{array} \)
\( (3-\lambda) \cdot(0-\lambda) \cdot(3-\lambda) \cdot 2 \cdot 2 \cdot 4+4 \cdot 2 \cdot 2-(4 \cdot(0-\lambda) \cdot 4)-2 \cdot 2 \cdot(3-\lambda)-(3-\lambda) \cdot 2 \cdot 2 \)
\( (3-\lambda) \cdot(0-\lambda) \cdot(3-\lambda) \cdot(8+24 \lambda)=0 \)

Problem/Ansatz:

Answer 1

Im Zweifel multiplizierst du alles aus und fasst es zusammen

(3 - k)·(-k)·(3 - k) + 2·2·4 + 4·2·2 - 4·(-k)·4 - 2·2·(3 - k) - (3 - k)·2·2

= - k³ + 6·k² + 15·k + 8

Eine Wertetabelle ergibt die Nullstellen -1 ohne Vorzeichenwechsel und 8 mit Vorzeichenwechsel. Also ist die Faktorzerlegung

= - (k + 1)^2·(k - 8)

Schwierig würde es werden wenn nicht mal eine Nullstelle ganzzahlig ist. Aber dann hat man eh Schwierigkeiten mit einer Faktorisierung.

Comments

Danke dir Mathecoach!

Aber kann man das ganze nicht schöner zusammenfassen? Wenn iman das ganze ausmultipliziert, verrechnet man sich leicht. Unser Prof. meinte, dass wir das mit dem ausmultiplizieren lassen sollen. Nur wenn man keine andere Möglichkeit hat, sollte man ausmultiplizieren. Kann ich hier irgendwelche Klammern herausheben?

---

Zumindest nicht so einfach. Und in den Fällen finde ich das ausmultiplizieren einfacher als wenn du anfängst zu schieben. Das ausmultiplizieren ist hier wegen der binomischen Formel auch sehr einfach.

---

Okay, danke dir! Ich werde noch weitere Aufgaben durchrechnen, mal sehen, ob ich auf das richtige Ergebnis komme.