Wendepunkt berechnen. f'(t)=0=1,4(e^-0,02t-e^-0,04t)

Question

ok ich berechne den Wendepunkt in dem ich die erste Ableitung 0 setze und das Ergebnis in die zweite Ableitung einsetze und ausrechne?!

f'(t)=0=1,4(e^-0,02t-e^-0,04t) und e kann niemal 0 sein, also habe ich 1,4 und die sind auch =0?

f"(0)=0,028(2*e^-0,04*0-e^-0,02*0) =0,028....das kann doch nicht stimmen?!

Danke schon mal für Antworten!

Comments

Hattest du nicht im ersten Exponenten der Ableitung ein MINUS?

---

ja, hat sie ;)

---

 

wenn ich jetzt nicht total daneben liege:

1. Ableitung = 0; 2. Ableitung < 0 => Maximum, 2. Ableitung > 0 => Minimum an dieser Stelle.

Wendepunkt hingegen:

2. Ableitung = 0; 3. Ableitung ≠ 0

 

Deshalb bitte nochmals die Ursprungsfunktion f(x) angeben :-)

 

Besten Gruß

---

Danke, hier die Ursprungsfunktion

f(t)=0,3+35(1-e^-0,02t)

---

"Hattest du nicht im ersten Exponenten der Ableitung ein MINUS?"
"ja, hat sie ;)"

Na suuper!

Aber, die erste Ableitung von
f(t) = 35(1-e^{-0.02t}) + 0.3
ist
f'(t) = 0.7 e^{-0.02 t}

Das ist nicht die Ableitung, die du angegeben hast.
Und nun?

---

Hier war die ominöse Frage: https://www.mathelounge.de/87737/wie-bilde-ich-die-ableitung-richtig-f-t-0-3-35-1-e-0-02t-2

---

Ah, noch eine Variante der Stammfunktion! :D

---

Habe ich die Ursprungsfunktion in meiner Antwort falsch abgeschrieben?

Wenn nein, sollte Dir diese Antwort (siehe unten) Hilfe genug sein :-)

---

"Eure nicht ernst gemeinten Kommentare könnt ihr euch sparen."

Das war todernst gemeint! Nach jeder Nachfrage bezüglich deiner Aufgabenstellung kommst du mit einer neuen Variante der ersten Ableitung sowie der Stammfunktion, die noch nicht einmal zusammenpassen.

"Kann mir jetzt jemand helfen?"

Wenn du die Aufgabe richtig formulierst, bzw. abtippst, sodass Stammfunktion, Ableitung und deine Fragen bezüglich der Aufgabe stimmig sind, dann sicherlich.

---

Mensch, wenn ich hier eine Stammfunktion angegeben hab dann weiß ich nichts davon.

Grundsätzlich braucht man doch nur die zweite Ableitung und die dritte Ableitung um meineserachtens den Wendepunkt zu berechnen.

Das war letztlich meine Frage oder:

f"(t)(0)=0,028(2*e^-0,04*0-e^-0,02*0) =0,028....das kann doch nicht stimmen?!s.o.


Funktion lautet:     f(t)=0,3+35(1-e^-0,02t)^2

                                 f'(t)= 1,4(e^-0,02t-e^-0,04)

                                 f"(t)=0,028(2e^-0,04t-e^-0,02t)


Die Funktion und die erste und zweite Ableitung stehen als Kontrolle auf meinem Zettel!

Gesucht das stärkste Wachstum= Wendepunkt!

Answer 1

--------  Aufgrund wiederholt inkonsistenter Aufgabenstellung gelöscht ---------

Comments

Kann es sein das man einen Grenzwert oder Randbedingung berechnen muss und wenn ja,wie?

---

Sein kann so manches, Aufgabenstellung durchlesen und posten könnte weiterhelfen!

Answer 2

 

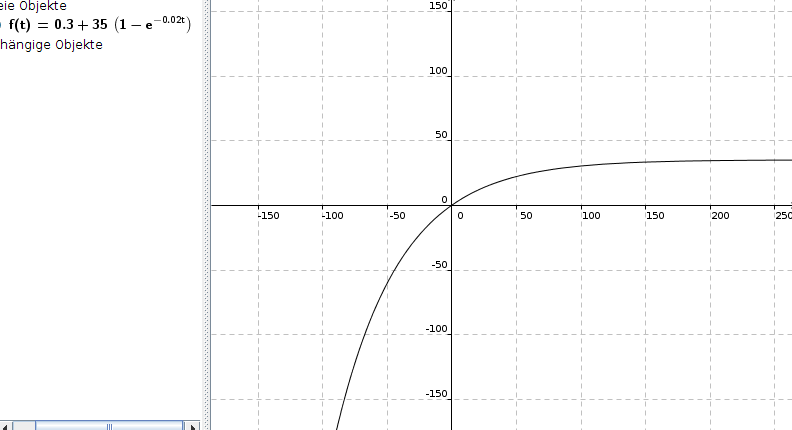
f(t) = 0,3 + 35 * [1 - e^{-0,02t}] = 0,3 + 35 - 35 * e^-0,02t

f'(t) = - 35 * (-0,02) * e^-0,02t = 0,7 * e^-0,02t

f''(t) = 0,7 * (-0,02) * e^-0,02t = -0,014 * e^-0,02t

f'''(t) = -0,014 * (-0,02) * e^-0,02t = 0,00028 * e^-0,02t

 

Wenn ich die Ursprungsfunktion richtig aufgeschrieben habe, sieht man hieraus:

Diese Funktion hat keine Wendestelle, denn f''(t) kann niemals = 0 werden, denn

-0,014 ≠ 0

e^-0,02t ≠ 0

 

Besten Gruß

Comments

Leider sind die Ableitungen laut meiner Lösung nicht übereinstimmend....

Angeblich soll die Funktion einen Wendepunkt besitzen.

Aber danke trotzdem!

---

Merkwürdig,

ich habe die Funktionsgleichung

f(t) = 0,3 + 35 * [1 - e^-0,02t] = 0,3 + 35 - 35 * e^-0,02t

zur Kontrolle in einen Online-Ableitungsrechner

http://www.ableitungsrechner.net/#

eingegeben, und der hat meine Berechnungen bestätigt.

Vielleicht sah die Ursprungsfunktion doch anders aus als die, mit der ich angefangen habe??

Und:

Gern geschehen :-)

Answer 3

 f(t)=0,3+35(1-e^-0,02t)²

                                 f'(t)= 1,4(e^-0,02t-e^-0,04)

                                 f"(t)=0,028(2e^-0,04t-e^-0,02t)

Setze die 2. Ableitung =0

 0,028(2e^-0,04t-e^-0,02t) =0           |: 0.028

2e^-0,04t-e^-0,02t =0               |e^-0.04t ausklammern

e^{-0.04t} (2 - e^{-0.02t + 0.04t}) =0

e^{-0.04t} (2 - e^{0.02t}) =0

Erster Faktor kann nicht 0 werden. 2. Faktor schon

2 = e^{0.02t}      |ln

ln(2) = 0.02t

ln(2) / 0.02 = t = 34.6574 ist der Kandidat für die Wendestelle. Kontrolle: 

https://www.wolframalpha.com/input/?i=2e%5E%28-0.04t%29-e%5E%28-0.02t%29+%3D0++

Setze  t = 34.6574 ein in f(t)=0,3+35(1-e^-0,02t)²

f(34.6574) =0,3+35(1-e^-(0,02*34.6574))²= 9.05001

Möglicher Wendepunkt:

WP(34.6574, 9.05001)

Comments

Boah du bist meine Rettung Lu!


Warum darf man den zweiten Faktor benutzen? Welches Gesetz?

---

Ein Produkt  ist genau dann 0 wenn einer seiner Faktoren Null ist.

---

Vielen Dank für die Lösung aber zwei Sachen verstehe ich nicht:

0,028(2e^-0,04t-e^-0,02t) =0           |: 0.028

2e^-0,04t-e^-0,02t =0               |e^-0.04t ausklammern

e-0.04t (2 - e-0.02t + 0.04t) =0  Warum ist hier plötzlich e^-0,02t Plus 0,04t?

e-0.04t (2 - e0.02t) =0 Und wieso darf man hier einfach die 0,04t dann wieder weglassen?

---

"e-0.04t (2 - e0.02t) =0 Und wieso darf man hier einfach die 0,04t dann wieder weglassen? "

e^{-0.04t } ist grösser als 0 für alle reellen t und kann daher gar nie 0 sein.