Wie bilde ich die Funktion vom Hoch- und Tiefpunkt?

Question

Aufgabe:Die Wendetangente an den Graphen einer ganzrationalen Funktion dritten Grades im Punkt P(0|1) besitzt die Steigung -24. Hoch- und Tiefpunkt der Funktion liegen jeweils zwei Einheiten von der y-Achse entfernt.

Problem/Ansatz:

Wie bilde ich die Funktion von dem Hoch- und Tiefpunkt?

Answer 1

Hallo

hoch und Tie fpunkt f'(2)=f'(-2)=0 ausserdem ist die funktion mit Wendepunkt in 0  punktsymmetrisch zum Punkt (0,1)

du hast für die Gleichung f(x) =ax^3+bx^2+cx+d  5 Gleichungen f(0)=1, f''(0)=0, f'(0)=-24 , f'(2)=0 f'(-2)=0

alles aufschreiben und das einfache linear GS für a,b,c,d lösen.

Gruß lul

Answer 2

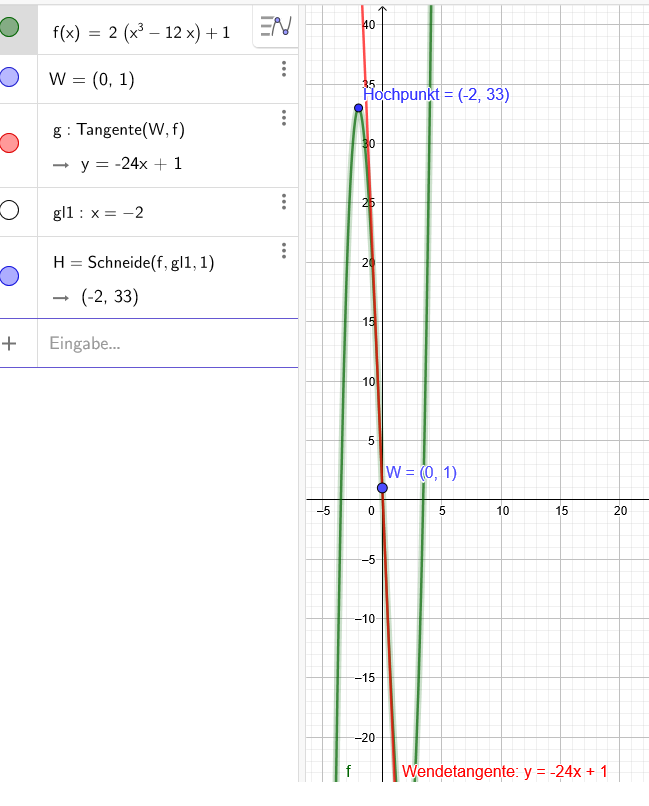
"Aufgabe: Die Wendetangente an den Graphen einer ganzrationalen Funktion dritten Grades im Punkt P(0|1) besitzt die Steigung -24. Hoch- und Tiefpunkt der Funktion liegen jeweils zwei Einheiten von der y-Achse entfernt."

Ich verschiebe den Graph um 1 Einheit nach unten: P´(0|0) →  Nullstellenform der kubischen Parabel

f(x)=a*x(x-N)*(x+N)=a*[x*(x^2-N^2)]=a*[x^3- N^2*x)]

Steigung -24 in P´(0|0)

f´(x)=a*[3x^2-N^2]

f´(0)=a*[-N^2]

1.)-a*N^2=-24  →a=\( \frac{24}{N^2} \)

H und T zwei Einheiten von der y-Achse entfernt.

f´(x)=\( \frac{24}{N^2} \)*[3x^2-N^2]

f´(2)=\( \frac{24}{N^2} \)*[3*2^2-N^2]

2.) \( \frac{24}{N^2} \)*[12-N^2]=0

12-N^2=0

N^2=12

a=\( \frac{24}{12} \)=2

f(x)=2*[x^3- 12*x)]

Nun wieder eine Einheit nach oben:

p(x)=2*[x^3- 12*x)]+1