Klausur Klasse 10. Suche ganzrationale Funktion vom Grad 3 durch A(2/2),B(3/9) und mit Tiefpunkt T(1/1).

Question

 bin neu hier und habe ein paar Fragen da ich bald meine nächste Mathearbeit schreibe. In der Arbeit soll ich Funktionsgleichungen verschiedener Grade bestimmen. Ein Teil muss mit dem Taschenrechner(Casio ClassPad 330) und ein Teil ohne gerechnet werden. Nun zu meinen Fragen
1. Wie bestimme ich eine ganzrationale Funktion vom Grad 2 deren Graph durch die Punkte A(1/3),B(-1/2),C(3/2) geht.
2.Ermittle jeweils eine ganzrationale Funktion vom Grad 3 deren Graph durch A(2/2),B(3/9) geht und den Tiefpunkt T(1/1) hat.

Das wars fürs erste^^ Ich hoffe ihr nehmt euch die Zeit um mir zu helfen. Ich möchte das wirklich verstehen. Danke schon im Voraus. MfG, Rafa

Comments

Schau vielleicht schon mal bei den 'ähnlichen Fragen' rein. Da kannst du bestimmt die Zahlen an deine Aufgaben anpassen. https://www.mathelounge.de/34938/ganzrationale-funktion-dritten-grades-tiefpunkt-verlauft

Schreibe einen Kommentar, wie weit du so kommst, falls du doch noch stecken bleibst.

Answer 1

1. Wie bestimme ich eine ganzrationale Funktion vom Grad 2 deren Graph durch die Punkte A(1/3),B(-1/2),C(3/2) geht.

Wenn man schlau ist erkennt man das beim Punkt B und C die Y-Koordinaten gleich sind. Daraus folgt das die X-Koordinate des Scheitelpunktes zwischen deren x-Werten liegt

Sx = (-1 + 3)/2 = 2/2 = 1

Wenn der Scheitelpunkt bei Sx = 1 liegt ist A der Scheitelpunkt der Parabel. Damit habe ich also den Scheitelpunkt und einen weiteren Punkt und kann die Scheitelpunktform aufstellen.

Öffnungsfaktor 

a = (Py - Sy) / (Px - Sx)^2 = (2 - 3) / (3 - 1)^2 = -1/4

Scheitelpunktfom der Parabel

f(x) = a*(x - Sx)^2 + Sy = -1/4*(x - 1)^2 + 3

Skizze

Comments

Weil das ganze jetzt mit Trick 17 möglichst schnell gerechnet worden ist hier noch ein allgemeiner Weg, der aber etwas rechenintensiver ist.

1. Wie bestimme ich eine ganzrationale Funktion vom Grad 2 deren Graph durch die Punkte A(1/3), B(-1/2), C(3/2) geht.

Allgemeiner Ansatz der Funktion

f(x) = ax^2 + bx + c

f(1) = 3 --> a + b + c = 3
f(-1) = 2 --> a - b + c = 2
f(3) = 2 --> 9a + 3b + c = 2

Dieses LGS löst man. Stichwort Additionsverfahren. Notfalls mit dem Casio.

a = - 1/4 ∧ b = 1/2 ∧ c = 11/4

Damit lautet die Funktion

f(x) = - 1/4·x^2 + 1/2·x + 11/4

---

2. Ermittle jeweils eine ganzrationale Funktion vom Grad 3 deren Graph durch A(2/2), B(3/9) geht und den Tiefpunkt T(1/1) hat.

f(x) = a·x^3 + b·x^2 + c·x + d
f'(x) = 3·a·x^2 + 2·b·x + c 

f(2) = 2 --> 8·a + 4·b + 2·c + d = 2
f(3) = 9 --> 27·a + 9·b + 3·c + d = 9
f(1) = 1 --> a + b + c + d = 1
f'(1) = 0 --> 3·a + 2·b + c = 0

Das LGS ergibt die Lösung: a = 1 ∧ b = -3 ∧ c = 3 ∧ d = 0

Damit lautet die Funktion

f(x) = x^3 - 3·x^2 + 3·x

Da das jetzt igendwie nicht hinhaut würde ich dich bitten die Aufgabenstellung nochmals genau zu kontrollieren.

Answer 2

Hallo Rafa,

 

1. Wie bestimme ich eine ganzrationale Funktion vom Grad 2 deren Graph durch die Punkte A(1/3),B(-1/2),C(3/2) geht?

Zuerst schreibst Du die allgemeine Form einer ganzrationalen Funktion 2. Grades hin:

f(x) = ax² + bx + c

Der Graph geht durch A(1|3), also

f(1) = 3 = a*1² + b*1 + c | a + b + c = 3

und durch B(-1|2)

f(-1) = 2 = a*(-1)² + b*(-1) + c | a - b + c = 2

und durch C(3|2)

f(3) = 2 = a*3² + b*3 + c | 9a + 3b + c = 2

3 Gleichungen, 3 Unbekannte, Lösung:

a = -0,25

b = 0,5

c = 2,75

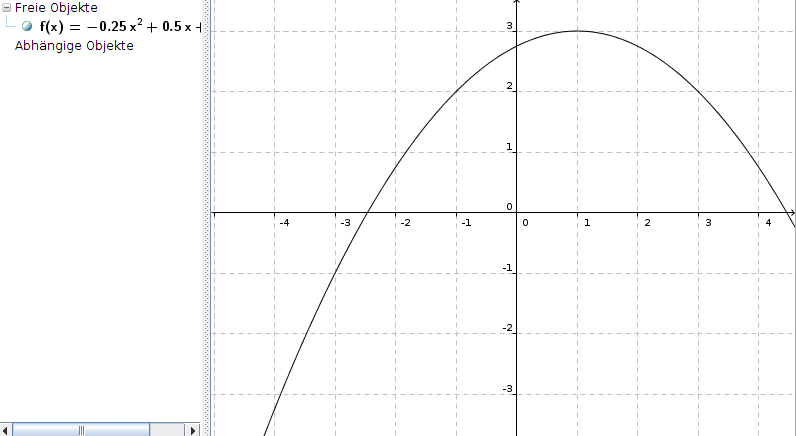
Die Funktion lautet also

f(x) = -0,25x² + 0,5x + 2,75

So sieht der Graph der Funktion aus:

 

2. Ermittle jeweils eine ganzrationale Funktion vom Grad 3 deren Graph durch A(2/2),B(3/9) geht und den Tiefpunkt T(1/1) hat.

Graph einer Funktion 3. Grades:

f(x) = ax³ + bx² + cx + d

f'(x) = 3ax² + 2bx + c

f''(x) = 6ax + 2b

Der Graph geht durch A(2|2):

f(2) = 2 = 8a + 4b + 2c + d

Der Graph geht durch B(3|9):

f(3) = 9 = 27a + 9b + 3c + d

Er geht durch T(1|1):

f(1) = 1 = a + b + c + d

Er hat dort einen Tiefpunkt, also Steigung = 0:

f'(1) = 0 = 3a + 2b + c

4 Gleichungen, 4 Unbekannte, Lösung:

a = 1

b = -3

c = 3

d = 0

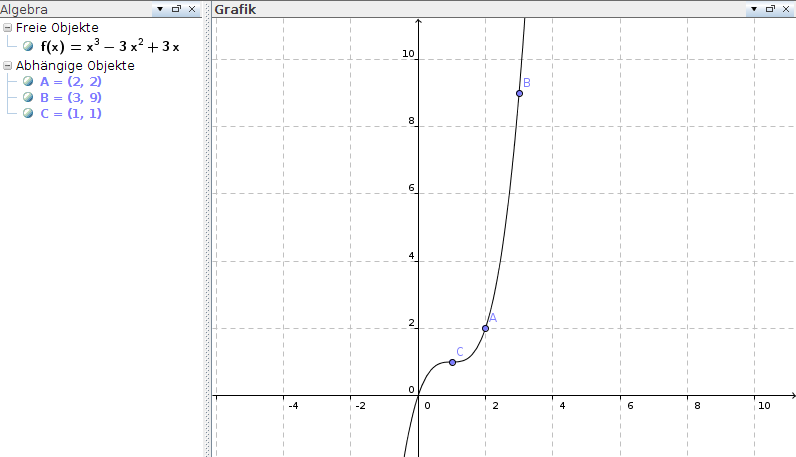
Die Funktion lautet also:

f(x) = x³ - 3x² + 3x

In T(1|1) hat der Graph aber keinen Tiefpunkt, sondern einen Sattelpunkt (ich hoffe, es hilft trotzdem):

Besten Gruß

Comments

Vielen dank hat mir sehr geholfen. Und die Aufgabe steht genauso auf dem Blatt ich werde mal meinen Lehrer fragen und nochmals vielen dank.

---

Das freut mich sehr!

Weiter viel Erfolg, und wenn Du irgendwann eine neue Frage hast:

Hier findest Du praktisch immer jemanden, der Dir gerne hilft :-D

Answer 3

2. Ermittle jeweils eine ganzrationale Funktion vom Grad 3 deren Graph durch \(A(2|2)\),\(B(3|9)\) geht und den Tiefpunkt \(T(1|1) \)hat.

Verschiebung um eine Einheit nach unten

\(T(1|1) \)→  \(T´(1|0) \)

\(f(x)=a(x-1)^2(x-N)\)

\(A(2|2)\)→\(A´(2|1)\)

\(f(2)=a(2-1)^2(2-N)=a(2-N)\)

\(a(2-N)=1\)→\(a=\frac{1}{2-N}\)

\(f(x)=\frac{1}{2-N}(x-1)^2(x-N)\)

\(B(3|9)\)→\(B´(3|8)\)

\(f(x)=\frac{1}{2-N}(3-1)^2(3-N)=\frac{4(3-N)}{2-N}\)

\(\frac{4(3-N)}{2-N}=8\) →  \(\frac{3-N}{2-N}=2\)      \(N=1\)      \(a=\frac{1}{2-1}=1\)

\(f(x)=(x-1)^2(x-1)\)

Verschiebung um eine Einheit nach oben:

\(p(x)=(x-1)^2(x-1)+1\)

An der Stelle \(x=1\) ist statt des Tiefpunktes ein Sattelpunkt.