ganzrationale Funktion: Grad 4, Sattelpunkt im Ursprung, Tiefpunkt P (-2|-6)

Question

Aufgabe:

Bestimmen sie die ganzrationale Funktion f mit den angegebenen Eigenschaften: Grad 4, Sattelpunkt im Ursprung, Tiefpunkt P (-2|-6)

Problem/Ansatz:

?

Answer 1

die Bedingungen lauten:

Sattelpunkt im Ursprung

f(0)=0
f'(0)=0
f''(0)=0

Tiefpunkt P (-2|-6)

f(-2)=-6
f'(-2)=0

Comments

Und wie geht es weiter?

---

Die Werte in die allgemeine Form \(f(x)=ax^4+bx^3+cx^2+dx+e\) bzw. seine Ableitungen einsetzen.

Danach erhältst du ein LGS, dass du dann lösen musst.

Hier werden aber die Koeffizienten c,d,e entfallen.

---

Wie genau lauten dann die Ergebnisse bzw. Zwischenergebnisse beim Einsetzen?

---

Bsp. Tiefpunkt:

\(f(-2)=-6 \rightarrow a(-2)^4+b(-2)^3+c(-2)^2+d(-2)+e=-6 \Leftrightarrow 16a - 8b + 4c - 2d + e = -6\\ f'(-2)=0 \rightarrow 4a(-2)^3 +3b(-2)^2+2c(-2)+d=0 \Leftrightarrow -32a + 12b - 4c + d = 0\)

---

Ist f(x)= 9/8x^4 + 3x^3 richtig?

---

Ist \(f(x)= \dfrac{9}{8}\cdot x^4 + 3\cdot x^3\) richtig?

Ja, das ist richtig.

Answer 2

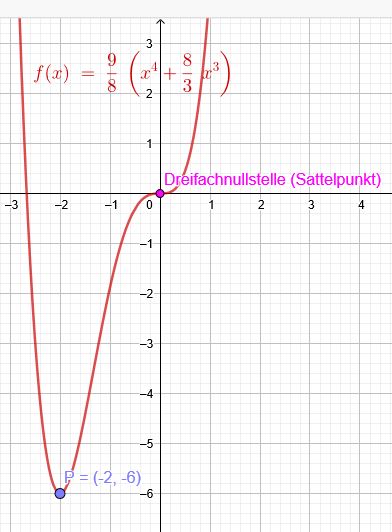
Bestimmen sie die ganzrationale Funktion f mit den angegebenen Eigenschaften: Grad 4, Sattelpunkt im Ursprung, Tiefpunkt P \((-2|-6)\)

Sattelpunkt im Ursprung bedeutet, da dort eine dreifache Nullstelle ist:

\(f(x)=ax^3(x-N)=a(x^4-Nx^3)\)

\(f'(x)=a(4x^3-3Nx^2)\)

Tiefpunkt P \((-2|...)\)   waagerechte Tangente:

\(f'(-2)=a(-32-12N)=0\)

\(N=-\frac{8}{3}\):

\(f(x)=a(x^4+\frac{8}{3}x^3)\)

P \((-2|-6)\):

\(f(-2)=a(16-\frac{64}{3})=-6\)

\(a=\frac{9}{8}\):

\(f(x)=\frac{9}{8}(x^4+\frac{8}{3}x^3)\)