Hallo,
wenn dort steht $$f:\space \mathbb R\times \mathbb R \to \mathbb R$$dann bedeutet das, dass es eine Funktion \(f\) gibt, die als Parameter zwei beliebige Zahlen akzeptiert und als Ergebnis eine Zahl liefert. Alternativ könnte dort auch stehen \(f:\space \mathbb R^2 \to \mathbb R\). Das ist das gleiche.
Stelle Dir das ganze als ein Höhenbild vor. Du hast eine Landkarte vor Dir, und dort ist ein Koordiatensystem eingezeichnet. Die \(x\)-Koordinate gibt an, wie weit sich ein mit \((x,\,y)\) bezeichneter Punkt im Osten befindet. Und die \(y\)-Koordinate gibt die Entfernung nach Norden vor. Für jeden Punkt \((x,\,y)\) lässt sich nun eine Höhe des Geländes über Normalnull angeben. Das ist der Wert den die Funktion \(f\) liefert.
Im konkreten Fall ist$$f(x, y)= xy −y^2$$und das 'Höhenbild' von \(f\) sieht so aus:
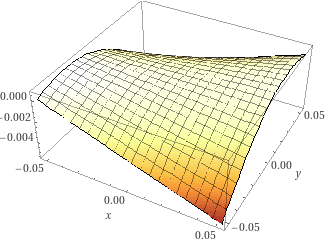
Für jeden Punkt \((x,\,y)\) gibt es genau einen (Höhen-)Wert. Es gibt keine Einschränkungen für den Zahlenbereich von \(x\) und/oder \(y\).
Was ist \(f ^{−1}([0, 1])\)? (Ohne Begründung.)
Heißt, es ist die Gegend (also ein wahrscheinlich eingeschränkter Bereich der Positionen \((x,\,y)\)) gesucht, wo die Höhe im Gelände zwischen \(0\) und \(1\) liegt. Wobei wir hier ein geschlossenes Intervall \([0,\,1]\) haben, also das Gelände mit der Höhe \(0\) und das mit Höhe \(1\) gehört noch dazu.
Wie findet man die gesuchte Gegend? Na ja, im einfachsten Fall, indem man sich auf gut Glück ein paar Positionen anschaut und ihre Höhe berechnet. Setze doch \(y\) mal auf \(y=1\), dann ist $$f(x,1) = x-1$$oder \(y=2\), \(y=3\) und andere Werte.
Für \(y=1\) muss \(x\) im Intervall \(x\in[1;\,2]\) liegen und für \(y=2\) im Intervall \(x\in[2;\,2,5]\). Mit höheren \(y\)-Werten wird es fü \(x\) enger. Probiere mal \(y=0,5\) und zeichne diese und weitere Strecken in ein Koordinatensystem ein:
~plot~ 1+0*ln(x-1)+0*ln(2-x);2+0*ln(x-2)+0*ln(2.5-x);0.5+0*ln(x-0.5)+0*ln(2.5-x);[[-3|4|-2|3]] ~plot~
Dann könnte man auf die Idee kommen, dass die Grenzen interessant sind. Also wo ist denn \(xy-y^2=0\) und \(xy-y^2=1\)? Überlege mal selber und das Bild dazu, liefere ich Dir noch:
$$g: \space\mathbb R \to \mathbb R\times\mathbb R,\quad g(x) = (3x, 7)$$
Hier ist es genau umgekehrt, wie \(f\). Bei \(g\) wir einem Parameter (einer Zahl) \(x\) ein Zahlenpaar \((3x,7)\) zugeordnet. Wenn ich das wieder als Landkarte auffasse, so liefert \(g\) nur den Ort an der Ost-Position \(3x\) und der Nord-Position \(7\). Sonst gar nichts.
Frage bitte möglichst konkret nach, wenn etwas unklar ist.
Gruß Wener