Vom Duplikat:
Titel: Umkehrfunktion bestimmen bei Abbildung
Stichworte: umkehrfunktion,definitionsbereich,ableitungen,exponentialfunktion,wurzeln
Aufgabe:
Aufgabe 1.
Es sei f : R+0 →(0,1] die Funktion
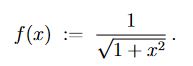
Text erkannt:
\( f(x):=\frac{1}{\sqrt{1+x^{2}}} \)
Problem/Ansatz:
Bestimmen Sie die Umkehrfunktion f−1 von f, und zeigen Sie durch Berechnen von f◦f−1
und f−1◦f, dass f−1 auch tatsächlich die Umkehrfunktion ist. Achten Sie insbesondere auf
Definitions- und Wertebereiche. (Durch den Nachweis der Existenz einer Umkehrfunktion
haben Sie dann auch automatisch gezeigt, dass f bijektiv ist.)