Geometrie - Berechnungen am Trapez

Question

Aufgabe:

Gegeben ist ein Trapez ABCD mit den Grundseiten (AB) und (CD).

Es gilt: a=8cm d=6cm α=60° β=80°

a) Zeige durch rechnung, dass gilt: c=4,08cm

b) Der Punkt M ist Mittelpunkt der Strecke AD. Zeichne das Dreieck BCM

c) Zeige dass gilt: BM= 7cm CM= 6,16 cm BC= 5,28 cm

d) Berechne den Flächeninhalt A des Dreiecks BCM. (Ergebnis: A=15,7 cm)

Answer 1

Hallo,

mache eine Planfigur und markiere die Vorgaben grün.

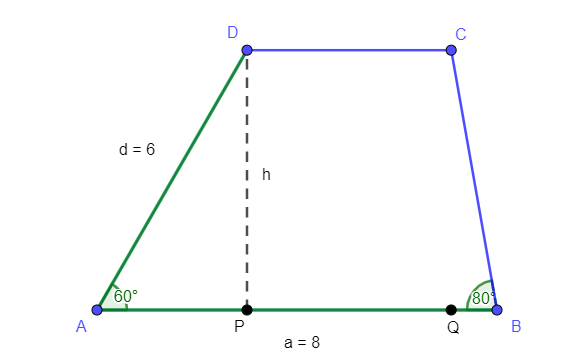
Wenn du die Strecken AP und QB von a = 8 abziehst, erhältst du die Länge der Strecke c = DC

APD und QBC sind rechtwinklige Dreiecke.

Die Strecke AP kannst du berechnen mit

\(cos(\alpha)=\frac{\text{Ankathete}}{\text{Hypotenuse}}\\cos(60)=\frac{AP}{6}\)

h mit \(sin(\alpha)=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}\\sin(60)=\frac{h}{6}\), was dir hilft, die Strecke QB zu berechnen.

Falls du noch Fragen hast, melde dich.

Gruß, Silvia

Comments

und wie soll ich jetzt BM CM und BC rechnen?

---

und wie soll ich jetzt BM CM und BC rechnen?

Suche nach rechtwinkligen Dreiecken:

\(|BC|\) ist die Hypotenuse von \(\triangle QBC\). Daraus folgt: $$|BC| = \frac{h}{\cos(80°)}$$\(|BM|\) ist die Hypotenuse von \(\triangle P_2BM\). \(|P_2M| = h/2\) und \(|P_2B| = c - |AP|/2\). Alles zusammen gefasst:$$|BM| = \sqrt{\left(\frac h2\right)^2 +\left(c - \frac 12 d\cos(60°)\right)^2}$$und das rechtwinklige Dreieck zu finden, dessen Hypotenuse die Strecke \(MC\) ist, überlasse ich Dir.

Ansonsten noch mal nachfragen!