Wie hoch muss er das Zelt bauen, wenn dessen Volumen möglichst groß sein soll?

Question

Aufgabe: Ein Pfadfinder baut aus einer Zeltplane mit den Maßen 2m x 2m einen einfachen zeltartigen Wetterschutz auf, der auf der Vorder- und der Rückseite offen ist. Wie hoch muss er das Zelt bauen, wenn dessen Volumen möglichst groß sein soll?

Problem/Ansatz: Bitte Lösung und Rechenweg notieren und erläutern, danke im voraus

Answer 1

Ich weiß nicht ob meine Vorstellungen so richtig sind.
Die Zeltform ist die eines Satteldachs.

die Tiefe 2m wird nicht gebraucht.

Die Vorderfront sieht so aus ?

h^2 + a^2 = 1^2  = > a^2 = 1^2 - h^2 => a = √ ( 1 - h^2 )
A = a * h
A = √ ( 1 - h^2 ) * h
A ´( h ) = √ ( 1 - h^2 ) - h^2 / [ √ ( 1 - h^2 ) ]
Extremwert
√ ( 1 - h^2 ) - h^2 / [ √ ( 1 - h^2 ) ] = 0
h = 0.707
Einsetzen
h^2 + a^2 = 1^2
0.707^2 + a^2 = 1
a = 0.707

Answer 2

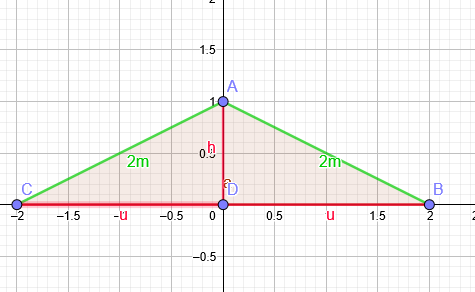
Aufgabe: Ein Pfadfinder baut aus einer Zeltplane mit den Maßen 2m x 2m einen einfachen zeltartigen Wetterschutz auf, der auf der Vorder- und der Rückseite offen ist. Wie hoch muss er das Zelt bauen, wenn dessen Volumen möglichst groß sein soll?"

Dreiecksäule:

Fläche Dreieck ABC:  \( \frac{2u}{2} \)*h=u*h

Volumen: V=2u*h soll maximal werden (weil das Zelt 2m lang ist)

u^2+h^2=4  → h^2=4-u^2   → h=\( \sqrt{4-u^2} \)

V=2u*\( \sqrt{4-u^2} \)=\( \sqrt{4u^2*(4-u^2)} \)=\( \sqrt{(16u^2-4u^4)} \)

\( V^{\prime}=\frac{32 u-16 u^{3}}{2 \cdot \sqrt{16 u^{2}-4 u^{4}}}=\frac{16 u-8 u^{3}}{\sqrt{16 u^{2}-4 u^{4}}} \)

\( \frac{16 u-8 u^{3}}{\sqrt{16 u^{2}-4 u^{4}}}=0 \rightarrow \) wobei der Nenner \( \neq 0 \)

\( 16 u-8 u^{3}=0 \)

\( 2 u-u^{3}=0 \)

\( u \cdot\left(2-u^{2}\right)=0 \)

\( u_{1}=0 \rightarrow \) minimales Volumen

\( u^{2}=2 \)

\( u=\sqrt{2} \)

h=\( \sqrt{4-2} \)=\( \sqrt{2} \)

Comments

A B muss 1m lang sein, dank georgborn!!

---

Praktischer Tip
Was kann man machen falls man vor einer Flugreise Angst hat im Flugzeug könnte eine Bombe versteckt sein?
Man nimmt auch eine Bombe mit.
Die Wahrscheinlichkeit das in einem
Flugzeug 2 Bomben sind ist
nahezu null.