Welche Abmessungen hat das Rechteck, wenn die Fläche möglichst groß sein soll?

Question

Aufgabe:

Eine Glasscheibe hat die Form eines rechtwinkligen Dreiecks mit den Kathetenlängen von 80cm und 100cm. Aus dieser Glasscheibe soll eine rechteckige Scheibe für einen Bilderrahmen geschnitten werden.

Welche Abmessungen hat das Rechteck, wenn die Fläche möglichst groß sein soll?

Answer 1

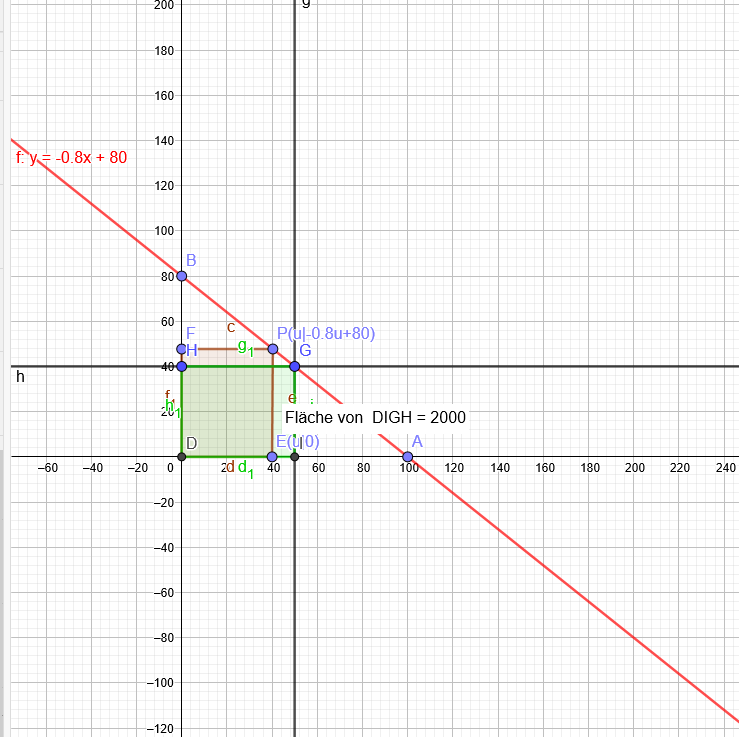
f(x)=-0,8x+80

f(u)=-0,8u+80

A(u)=u*f(u) soll maximal werden.

A(u)=-0,8u^2+80u

\( \frac{dA(u)}{du} \)=-1,6u+80

-1,6u+80=0

u=50   f(50)=-0,8*50+80 =40

Maximale Fläche ist 2000FE

Das Rechteck könnte auch so gelegt werden, dass eine Seite auf y=-0,8x+80 liegt.

Comments

Bei diesen Aufgaben z.B. max Rechteck in
einer Dachschräge ist die Antwort immer
( Kathete1 / 2 ) * ( kathete2 /2 ) =
( 100 / 2 ) * ( 80 /2 ) = 50 * 40 = 2000 FE