Hallo,
mache Dir zunächst eine Skizze:
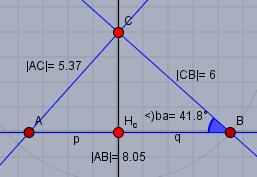
Gegeben sind \(h_c=4\) und \(a=|BC|=6\). Im Dreieck \(\triangle BCH_c\) gilt$$q^2 + h_c^2 = a^2 \\ \sin(\beta) = \frac{h_c}{a}$$so kommst Du zu \(q\) und \(\beta\).
nach dem Höhensatz gilt$$h_c^2 = p\cdot q \implies p = \frac{h_c^2}{q}$$und \(c=p+q\) und die Seite \(b\) folgt aus dem bekannten Pythagoras.
Die Ergebnisse kannst Du der Zeichnung entnehmen.
Gruß Werner