Parabelgleichung: S(2|4) P(5|-5)

Question

 Ich verstehe das Theman Quadratische Funktionen eigentlich schon, aber wenn es um die bestimmung der Funktion geht, weiß ich es nicht bzw. komme ich nicht weiter.
Bitte ausführlich erklären, wir schreiben in einer Woche eine Arbeit!
Gruß und dnake im Voraus
Aylin

Answer 1

Parabelgleichung: S(2|4) P(5|-5)

a = (Py - Sy)/(Px - Sx)^2 = (-5 - 4)/(5 - 2)^2 = -9/3^2 = -1

f(x) = a * (x - Sx)^2 + Sy = -1 * (x - 2)^2 + 4 = - x^2 + 4·x

Skizze

Comments

Diesen Lösungsweg also diese Formel zur bestimmung von a :)

---

Das geübte Auge erkennt hier einen Zusammenhang zur Steigungsformel einer linearen Funktion. Dort wird im Nenner nur nicht das Quadrat genommen.

---

ja das ist ja diese formel: m=y₂-y₁/x₂-x₁ :)

---

Genau. allerdings sollte man wenn man das hier hintereinander schreibt immer Klammern setzen.

Answer 2

Hallo Aylin,

 

wir haben gegeben den Scheitelpunkt S(2|4) und einen Punkt des Funktionsgraphen P(5|-5).

Eine quadratische Funktion lautet allgemein:

f(x) = ax² + bx + c

Im Scheitelpunkt ist die 1. Ableitung = 0, also

f'(x) = 2ax + b = 0

Wir setzen S ein:

f'(2) = 2a*2 + b = 0 | 4a + b = 0

Außerdem liegt S(2|4) natürlich auf dem Graphen, deshalb:

f(2) = 4a + 2b + c = 4

Wir setzen P in f(x) ein:

f(5) = a*25 + b*5 + c = -5, also 25a + 5b + c = -5

 

Wir erhalten

a = -1

b = 4

c = 0

 

Die gesuchte Funktion lautet also:

f(x) = -x² + 4x

 

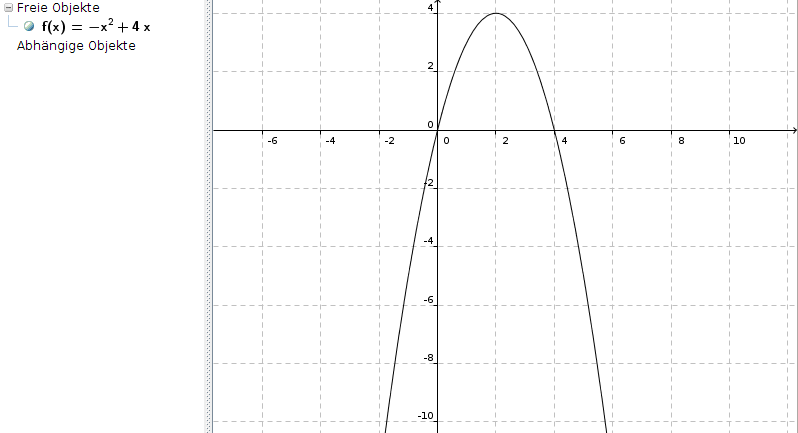
Ich hoffe, das hilft ein wenig :-)

 

Besten Gruß

Comments

Hallo :-)

Sehr schöne und ausführliche Erklärung..aber wir haben noch ableitung oder so nicht???? wir haben das auch so gar nicht gemacht?? ich bin in der realschule :)

könntest du es mir vielleicht noch anders erklären ohne ableitung? du erklärst das nämlich so ausfürhlich :)

---

Würde ich gerne, muss mich aber selbst noch in die Scheitelpunktform einarbeiten :-(

Deshalb bitte ich Dich, die Antworten vom Mathecoach und von Emre anzuschauen und zu verarbeiten :-)

---

Habe eben folgendes gefunden:

http://nibis.ni.schule.de/~rs-hoha/Homepage/dateien/UmwandlungAllgemeineFormS-P-Form.pdf

Da P "unterhalb" von S liegt, kann man die Vorgehensweise bei

"Parabel nach unten geöffnet!"

nutzen :-)

---

hi nochmal :)

ich habs jetzt endlich verstanden!!! und danke für den link der ist sehr gut!!!
jetzr steht nicht mehr im wege  :)

aber wem soll ich jetzt den stern geben?

---

Gern geschehen!

Stern für Emre war eine gute Wahl (ganz im Ernst!) :-)

Answer 3

Hi Aylin, 

S(2|4) P(5|-5)

a= (Py-Sy)/(Px-Sx)² 

a= (-5-4)/(5-2)² = (-9)/(3)²=-1 

f(x)=a*(x-xs)²+s_y = -1(x-2)²+4 =-1x²+4x 

f(x) = -1x²+4x
 

Grüße 

 

Comments

Hallo...

dankee ich habs verstanden...is eingentlich gar nicht so schwer...aber am anfang hatte ich damit probleme und jetzt nicht mehr. dannke <3

---

bitte bitte :)