Aufgabe:
Zeigen Sie
A\∪m∈MBm = ∩m∈MA\Bm, A\∩m∈MBm = ∪m∈MA\Bm
für eine Indexmenge M
Problem/Ansatz:
Ich weiß, wie ich das zweite lösen kann.
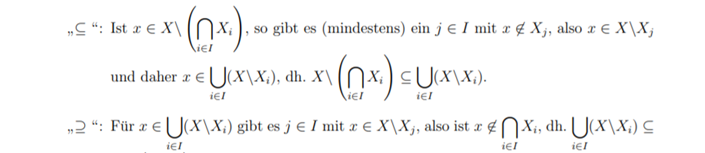
Text erkannt:
"\subseteq ": Ist \( x \in X \backslash\left(\bigcap_{i \in I} X_{i}\right) \), so gibt es (mindestens) ein \( j \in I \) mit \( x \notin X_{j} \), also \( x \in X \backslash X_{j} \) und daher \( x \in \bigcup_{i \in I}\left(X \backslash X_{i}\right) \), dh. \( X \backslash\left(\bigcap_{i \in I} X_{i}\right) \subseteq \bigcup_{i \in I}\left(X \backslash X_{i}\right) \)
"\supseteq ": Für \( x \in \bigcup_{i \in I}\left(X \backslash X_{i}\right) \) gibt es \( j \in I \) mit \( x \in X \backslash X_{j} \), also ist \( x \notin \bigcap_{i \in I} X_{i} \), dh. \( \bigcup_{i \in I}\left(X \backslash X_{i}\right) \subseteq \)
Kann ich das erste parallel dazu machen?