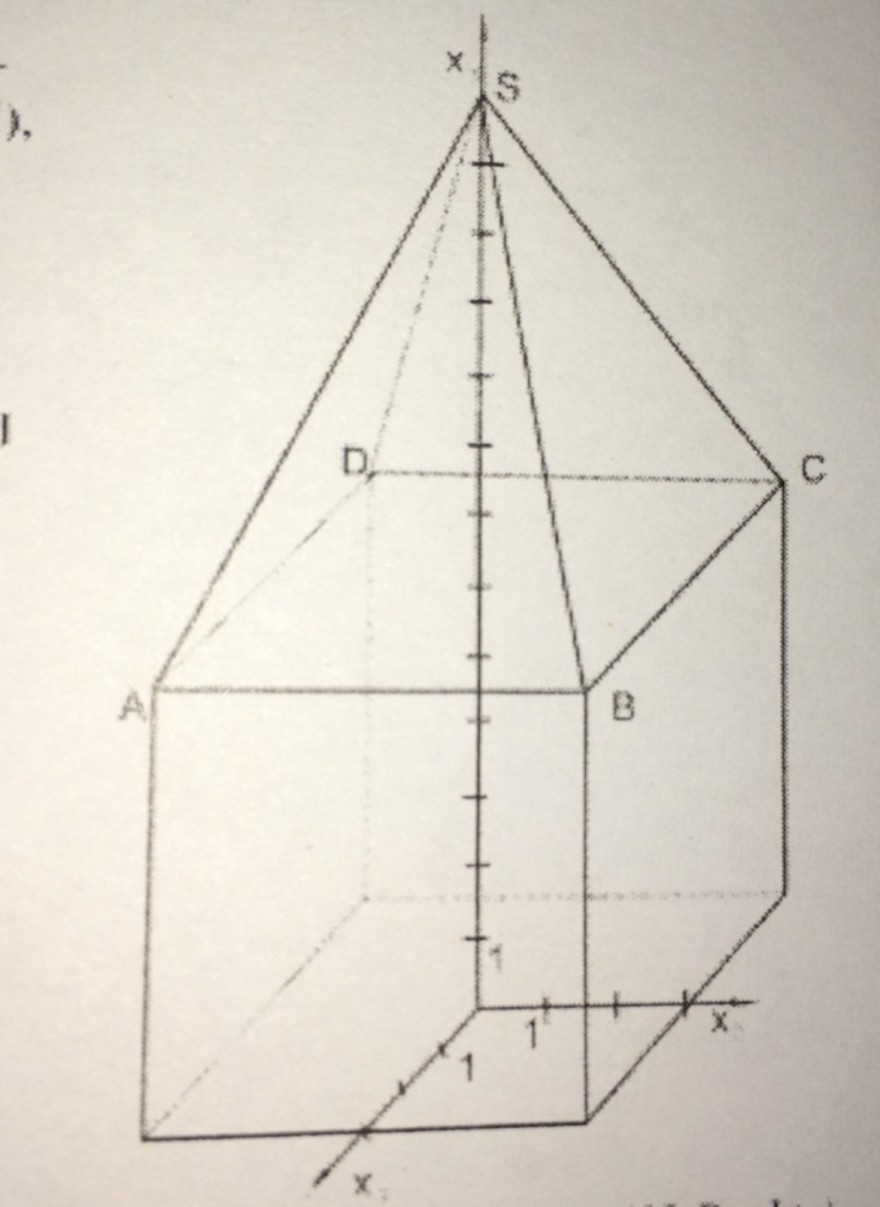
Schaubild + Kurze Erklärung etwas weiter unten geschrieben! :)
Aufgabe:
Auf einen Quader mit der Grundfläche in der x1-x2-Ebene ist eine Pyramide mit folgenden Eckpunkten aufgesetzt: A(3|-3|7), B(3|3|7), C(-3|3|7), D(-3|-3|7) und S(0|0|13)
Nun die Aufgaben:
a) Die Ebene E1 verläuft durch die Mitte der Pyramidenkanten SB bzw. SD und den Punkt C. Die Pyramidenkante AS liegt auf der Geraden g. (eigentlich sind die Striche bei SB, SD und AS über den Buchstaben, falls das wichtig ist).
1) Berechnen Sie eine Gleichung für die Ebene E1 in Parameterform.
2) Geben Sie eine Gleichung für die Gerade g an.
3) Zeigen Sie, dass die Gerade g die Ebene E1 rechtwinklig schneidet. Ermitteln Sie eine Gleichung der Ebene E1 in Koordinatenform.
b)
1) Zeigen Sie, dass es sich bei der Pyramide ABCDS um eine quadratische Pyramide handelt, und berechnen Sie das Volumen der Pyramide ABCDS.
2) Bestimmen Sie den Flächeninhalt der Mantelfläche der Pyramide.
c) Die Dreiecksfläche BCS liegt in der Ebene E2.
1) Berechnen Sie eine Gleichung der Ebene E2 in Koordinatenform und zeigen Sie, dass die Punkte F1(0|1|11), F2(1|2|9) und F3(-1|2|9) in der Ebene E2 liegen.
2) Zeigen Sie, dass das Dreieck F1F2F3 gleichschenklig ist.
d) die Gerade h ist durch folgende Gleichung gegeben: h: x = (0, 5, 15)+t*(-4, 11,14), t € R.
1) Bestimme Sie die Koordinaten des Durchstoßpunktes L der Geraden h mit der Ebene E2 aus der Teil Aufgabe C1
2) Weisen Sie nach, dass der Punkt L auf der Seitenkante BS des Dreiecks BCS liegt.
Problem/Ansatz:
Hey, hab nun alles gerechnet bis zum Aufgababenteil c). Ab da, also Aufgabenteil C) und D); Jeweils Aufgabe 1 und 2 bräuchte ich nun Hilfe. Wäre nett wenn mir jemand helfen könnte! Danke im Voraus! :)