Punkt an einer Geraden spiegeln

Question

Hallo, ich soll ein Dreieck an einer Geraden spiegeln.

Ich würde die drei Punkte, mit denen ich mein Dreieck konstruiert habe, jeweils an der Geraden spiegeln.

Problem: ich soll dies rechnerisch machen und ich finde wirklich nicht online dazu und mir fällt auch nichts dazu ein...

Es wurde dazu zzgl. geschrieben, dass es eine schwierige Aufgabe ist, also denke ich mal die Antwort wird nicht so simpel sein.

Falls jemand eine Ahnung hat würde ich mich sehr über eine Vorgangssbeschreiung freuen, da ich einfach keine Ahnung habe.

danke euch schon mal :)

Comments

gallo lola999,

kannst du vielleicht ein beispiel für punkte nenne

denn somit kann man es leichter erklären und besser nachvollziehen

:)LG

---

Ich habe unten, in dem Kommentar, einmal die Gerade gennant und einer der Punkte der gespiegelt werden sollte. Die anderen zwei Punkte würde ich dann gerne selbst machen.

Lieben Dank

Answer 1

Wenn du mir die Gerade und einen Punkt nennst, kann ich dir das gerne vormachen.

Comments

Die Gerade wäre y= -2x-3 und ein Punkt des Dreiecks ist z(8;-4).

Es würde mir eine allgemeine Beschreibung reichen, da ich das eigentlich selbst verstehen möchte.

Lieben Dank

---

Aber ist meine "Idee" richtig, es anhand meiner drei Konstruktionspunkte an der Geraden zu spiegeln?

---

Ja. Das grundsätzliche Vorgehen, dass du jeden Punkt spiegeln musst ist richtig.

Stelle zunächst die orthogonale zur Geraden durch den Punkt Z in der Punkt Steigungsform auf. Senkrecht zur Steigung m ist die Steigung -1/m.

y = 1/2 * (x - 8) - 4 = 1/2 * x - 8

Schneide beide Geraden

-2 * x - 3 = 1/2 * x - 8 --> x = 2

y = -2 * 2 - 3 = -7

S(2 | -7)

Spiegel jetzt den Punkt Z am Punkt S

Z'(2 * 2 - 8 | 2 * (-7) - (-4)) = Z'(-4 | -10)

Skizze

~plot~ -2x-3;1/2x-8;{8|-4};{2|-7};{-4|-10};[[-12|12|-12|2]] ~plot~

---

Zeichne dir das auch für die anderen Punkte damit du es Kontrollieren kannst.

Ich habe das jetzt rein über lineare Funktionen gemacht. Ich könnte das aber auch mit Vektoren machen.

---

Kannst du mir den erste Schritt und den letzten Schritt genauer erklären, bzw. wie du genauer auf die Werte kommst?

Vielen Dank, vielleicht habe ich gerade nur ein Brett vor dem Kopf und komme nicht drauf...

---

Also, ich meine wie kommst du auf die erste Gleichung  y=1/2(x-8)-4= 1/2x-8

---

y = 1/2 * (x - 8) - 4

1/2 ist die orthogonale Steigung zu -2, weil -1/(-2) = 1/2

Der Punkt (8 | -4) wird direkt in die Punkt-Steigungsform eingetragen. Ausmultiplizieren um zu vereinfachen solltest du können.

Wenn du Z an S spiegeln möchtest könntest du in Vektoren rechnen.

Z' = S + ZS = S + (S - Z) = 2·S - Z = 2·[2, -7] - [8, -4] = [-4, -10]

---

habe das selbst bei Geogebra gespiegelt und da kommen bei mir andere Werte heraus:(-8;-4).

---

Ich weiß nicht genau was du gemacht hast. Aber schau dir doch meine Skizze oben an.

https://www.mathelounge.de/885757/punkt-an-einer-geraden-spiegeln?show=885766#c885766

Answer 2

Hier eine symbolische Skizze

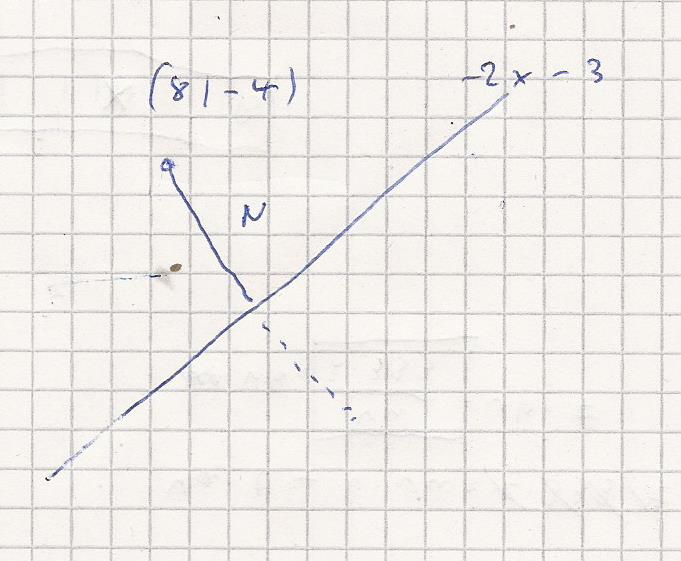
P ( 8 | -4 )
f ( x ) = -2x - 7

Die Steigung der Normalen N ( 90 ° zu f )
m = - 1 /(-2) = 1/2

Die Normale geht durch P
-4 = 1/2 * 8 + b
b = -8

N ( x ) = 0.5 * x - 8

Schnittpunkt der Geraden mit N

-2*x - 7 = 0.5 * x - 8
x = 0.4
y = -2*0.4 - 7 = -7.8
S ( 0.4 | -7.8 )

Jetzt ausrechnen welcher Abstand P zu S
delta x = | 0.4 - 8 | = 7.6
x auf der andern Seite durch Spiegelung
x = 0.4 - 7.6 = - 7.2

delta y = | -7.8 - ( - 4 | ) = 3.8
y auf der andern Seite durch Spiegelung
x = -7.8 - 3.8 =  -11.6

P2 ( -7.2 | - 11.6 )

Bitte nachfragen bis alles klar ist

Comments

Text erkannt:

\( f(x)=-2 x-7 \)
\( A=(8,-4) \)
\( \quad= \) Spiegle \( (A, y \) Ach \( \rightarrow(-8,-4) \) Eingabe....

sie har zwar eine andere Gleichung gehabt, aber egal. Ich habe es auch mal anhand deiner bei geogebra zeichnen lassen….

Macht geogebra es falsch oder wie ?

Vielleicht macht sie den gleichen Fehler wie ich?

---

Jup, ich habe es mir auch zeichnen lassen und es kommt auch dieser Punkt gespiegelt heraus.

Langsam glaube ich, ich habe da einen kompletten Denkfehler drin......

---

Ich kenne geobra nicht.
Dein linker Punkt ist falsch
Ich kann leider keine Punkte darstellen.
Bei meinem Graph sind die Endpunkte
die gesuchten Punkte