Punkt P an der Gerade spiegeln

Question

Aufgabe:

Eine Gerade g verläuft durch die Punkt A und B

Gegeben:

a.) A(-3(4) , B(5/-2), P(7/9)

b.) A(-2/-3), B(8/1), p(6/-8,5)

Gesucht:

-> Gib die Gleichung von g in Paramterdarstellung und in Normalvektorform an.

-> Spiegele den Punkt P an der Geraden und gib die Koordinaten des gespiegelten Punkts P* an.

Problem/Ansatz:

Ich hab die Paramterdarstellung und Normalvektorform berechnet und hoffentlich ist es auch richtig:

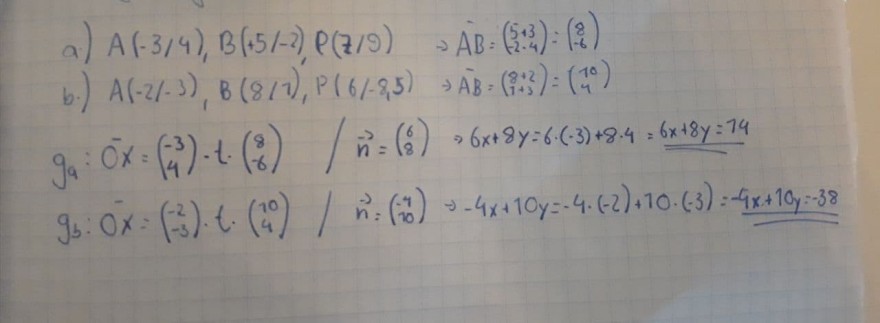
Text erkannt:

a) \( A(-3 / 4), B(+5 /-2), P(z / 9) \quad \rightarrow \quad A B=\left(\begin{array}{l}513 \\ 2.4\end{array}\right):\left(\begin{array}{l}8 \\ -6\end{array}\right) \)
b.) \( A(-2 /-3), B(8 / 7)^{\prime}, P(6 /-8,5) \rightarrow A_{B}=\left(\begin{array}{l}8+2 \\ 1+3\end{array}\right)=\left(\begin{array}{l}10 \\ 4\end{array}\right) \)
\( g_{9}: \bar{O}^{-} x=\left(\begin{array}{c}-3 \\ 4\end{array}\right) \cdot t \cdot\left(\begin{array}{c}8 \\ -6\end{array}\right) \quad \mid \vec{n}=\left(\begin{array}{l}6 \\ 8\end{array}\right) \quad \Rightarrow 6 x+8 y=6 \cdot(-3)+8 \cdot 4=6 x+8 y=14 \)

Dazu noch die ganzen Koordinaten:

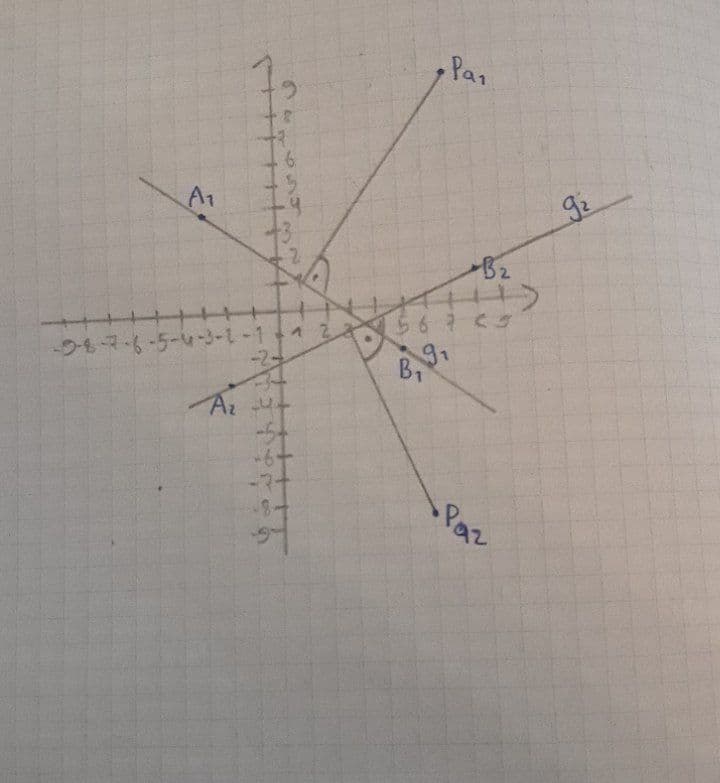
Leider weiß ich nicht wie ich den Punkt P spiegeln soll.

Answer 1

a) sieht dann wie folgt aus

Comments

Gibt es ein bestimmtes Formel dafür?

---

Du hast ja g bereits in Parameterform notiert

g: X = [-3, 4] + r * [8, -6]

Jetzt nimmst du dazu eine Senkrechte durch P

h: X = [7, 9] + s * [6, 8]

Ermittel jetzt den Schnittpunkt von g und h

[-3, 4] + r * [8, -6] = [7, 9] + s * [6, 8] --> r = 1/2 ∧ s = -1

Wenn du s = -1 einsetzt erhältst du den Lotfußpunkt auf der Geraden. Wenn du s = 2 * (-1) = -2 einsetzt erhältst du den Schnittpunkt

[7, 9] - 2 * [6, 8] = [-5, -7]

Vergleiche das mit der Skizze. Sieht also ganz gut aus.

---

Gibt es ein bestimmtes Formel dafür?

Ja - man muss 'nur' den Weg, den der Mathcoach beschritten hat, formal mit Variablen (und nicht mit Zahlen) aufschreiben.

Die Gerade, an der gespiegelt werden soll, muss in der Normalform gegeben sein$$\vec n \cdot \vec x = d$$dann ist das Spiegelbild \(P'\) eines Punktes \(P\)$$P' = \left( \underline 1 - \frac {2 \vec{n} \vec{n}^T}{|\vec{n}|^2} \right) P + \frac {2 d \vec n}{|\vec{n}|^2}$$Wobei \(\underline 1\) die Einheitsmatrix ist und \(\vec{n} \vec{n}^T\) das dyadische Produkt - also eine Matrix.

Hier bei Dir für die Gerade \(g\) in Koordinatenform \(3x+4y=7\)$$g:\quad \begin{pmatrix}3\\ 4\end{pmatrix}\vec x = 7, \quad \vec n=\begin{pmatrix}3\\ 4\end{pmatrix}, \quad d=7$$ist das konkret$$P' = \begin{pmatrix}0.28& -0.96\\ -0.96& -0.28\end{pmatrix} \cdot P+\begin{pmatrix}1.68\\ 2.24\end{pmatrix}$$Setze \(P(7|\, 9)\) mal ein und rechne es aus.

Answer 2

Hallo,

konstruiere eine Gerade, die durch P verläuft und senkrecht auf g steht. Bestimme den Schnittpunkt S der Geraden g und h. Addiere zu dem Schnittpunkt den Vektor PS.

Gerade h, die senkrecht auf g steht

[spoiler]

Der Normalenvektor zu g ist \(\vec{n}=\begin{pmatrix} 6\\8 \end{pmatrix}\)

\(h:\quad \vec{x}=\begin{pmatrix} 7\\9 \end{pmatrix}+r\cdot \begin{pmatrix} 6\\8 \end{pmatrix}\)

[/spoiler]

Jetzt die Geraden gleichsetzen und r oder t berechnen. Das Gleichungssystem

-3 + 8t = 7 + 6r

4 - 6t = 9 + 8r

ergibt r = -1.

Das in h einsetzen und den Schnittpunkt bestimmen.

[spoiler]

\(\begin{pmatrix} 7\\9 \end{pmatrix}+(-1)\cdot \begin{pmatrix} 6\\8 \end{pmatrix}=\begin{pmatrix} 1\\1 \end{pmatrix}=S\)

[/spoiler]

Das zu P addieren ergibt den Spiegelpunkt P'.

[spoiler]

\(PS=\begin{pmatrix} -6\\-8 \end{pmatrix}\\ P+\overrightarrow{PS}=\begin{pmatrix} 1-6\\1-8 \end{pmatrix}=\begin{pmatrix} -5\\-7 \end{pmatrix}\)

[/spoiler]

Gruß, Silvia