Stimmt die Oberfläche?

Question

Aufgabe:

Maße in cm

30 * 60 + 2 * ( 60 * 30 ) + 2 * [  (30 +60) / 2 * 30 ]= 8100cm^2= 81dm^2. Stimmt?

bin durcheinander

wie gross ist der Oberfläche (Blech)

Answer 1

Stirnseite       \( \frac{30+60}{2} \)·30

Rückseite      \( \frac{30+60}{2} \)·30

linke Wand    30·60

rechte Wand  34·60

Boden            30·60

______________________

                  8340 cm²= 83,4 dm².

Comments

Du hast die Maße wohl falsch abgelesen., ich komme auf ein Volumen von etwa 75,6 Liter.

---

Er hat ja auch vom Oberflächeninhalt geredet.

Volumen ist A_G·h.

Also V=\( \frac{30+60}{2} \)·30·60

---

Er hat ja auch vom Oberflächeninhalt geredet.

Er hat seine Volumenangabe (81000cm³) gelöscht, durch eine Flächenberechnung ersetzt aber den Fehler nicht korrigiert.

Vielleicht würde eine sinnvolle Bearbeitung der Aufgabe mit "Kann ich nicht" anfangen.

---

HAllo,

ich konnte das Volume berechnen.( 81L) es eght NUR um den Oberfläche.

Zitat Roland "rechte Wand 34·60" Wie bist du so gekommen? Warum nich auch wie linke Seite ( Wand)30 *60?

Lösung im Buch ist falsch , oder?

er hat die Wände mit 60 * 34 gerechnet, das ist aber falsch , oder?

Text erkannt:

10. a) \( 342 \mathrm{~cm}^{3} \)
b) \( 843,75 \mathrm{~m}^{3} \)
c) \( 10000 \mathrm{~cm}^{3} \)
d) \( 100 \mathrm{~m}^{3} \)
11. a) \( 60000 \mathrm{~cm}^{3}=60 \mathrm{dm}^{3}=60 \ell \) \( 7400 \mathrm{~cm}^{2}=74 \mathrm{dm}^{2} \)
Der Körper fasst \( 60 \ell \) und man benötigt \( 74 \mathrm{dm}^{2} \) Blech für die Hersuellung.
oder \( \mathrm{V}=60 \ell ; \mathrm{O}=74 \mathrm{dm}^{2} \)
b) \( \mathrm{V}=81 \ell \quad \mathrm{O}=85,8 \mathrm{dm}^{2} \)
c) \( \mathrm{V}=10,5 \ell \quad \mathrm{O}=25 \mathrm{dm}^{2} \)
12. \( 40572 \mathrm{~cm}^{3} ; 109544,4 \mathrm{~g} \approx 110 \mathrm{~kg} \)
13. a) \( 292,74 \mathrm{~m}^{3} \)
b) \( 357,14 \mathrm{~m}^{3} \)
c) \( 398,75 \mathrm{~m}^{3} \)
d) \( 484,42 \mathrm{~m}^{3} \)

---

er hat die Wände mit 60 * 34 gerechnet

Das hast du sehr gut erkannt !
Diese Rechnung ist auch richtig, aber es gibt einen Fehler in der Skizze.

Die rote Linie "30cm" soll die Höhe des Trapezes sein und nicht die Seitenlänge des linken Rechtecks, obwohl sie parallel zu dieser Rechteckseite gezeichnet ist. (In meiner oben angegebenen Lösung für das Volumen war ich von den Seitenlängen 30-34-60-30 des Trapezes ausgegangen und hatte die Höhe des Trapezes daraus berechnet.)
Außerdem fehlt der in der Skizze der Hinweis, dass das Trapez symmetrisch sein soll (es hat also tatsächlich die Seitenlängen 30-34-60-34), weil man das aus der Skizze nicht gut erkennen kann.

---

Roland Zitat" linke Wand   30·60

rechte Wand 34·60" warum mal 30 , mal 34?

sin d diese beide Seitenwände Rechteecke?

wenn ja dann verstehe jetzt

---

Die Seitenwände sind Rechtecke aber die linke Wand ist etwas breiter als 30 cm.

---

das meine ich , wenn stimmt dann versthe ich

Text erkannt:

II. Diek

---

So sieht das aus:

---

die linke Wand ist etwas breiter als 30 cm

Über 10% sind deutlich mehr als "etwas".

---

Ich fürchte, deine Kommentare verwirren den FS mehr, als dass sie ihm helfen. Willst du hier helfen oder deine zweifellos überragenden Fähigkeiten unter Beweis stellen?

---

Lies meinen Kommentar, darin findest du alle Hilfe, die du und der Fragesteller benötigen.

---

hallo, bin durcheinander

woher weißt du eine Seite ist 33,1  und andere 34 hoch?

Kannst du NUR linke( 1) und rechte (2) Wand als Rechteck zeichnen?

und warum die linke Wand nicht 30 cm hoch? Ist es 90 Grad, deswegen denke ich 30 cm hoch, oder?

so meine ich

Text erkannt:

(1) Linke wand
60

Text erkannt:

11. Die Körper sind oben offen. Wie viel Liter fasst deg. Körper? Wie thełm \( ^{2} \) Blech benötigt mar für die Herstellung (Maße in \( \mathrm{cm} \) )?

Text erkannt:

11. Die Körper sind oben offen. Wie viel Liter fasst deg. Körper? Wie thełm \( ^{2} \) Blech benötigt mar für die Herstellung (Maße in \( \mathrm{cm} \) )?

Text erkannt:

11. Die Körper sind oben offen. Wie viel Liter fasst dẹ Sörper? Wie Nict m \( ^{2} \) Blech benötigt mar für die Herstellung (Maße in \( \mathrm{cm} \) )?

---

x²+30²=34² oder x=\( \sqrt{34^2-30^2} \), also x=16

y=60-30-16=14

z²=14²+30² oder z=\( \sqrt{30^2+14^2} \), also z≈33,1.

---

Wirf mal einen Blick auf Aufgabe c) .

---

@hj2166: Wenn du etwas klären willst, dann benenne ganz deutlich, wo es klemmt. Bisher verwirrst du sowohl mich als auch den FS.

---

Ich habe oben alles ganz haarklein erklärt. Ihr müsstet das nur mal lesen und berücksichtigen.

Ein Blick auf Aufgabe c) könnte dir verraten, dass der Pythagoras offensichtlich noch gar nicht zur Verfügung steht, denn sonst müsste die Höhe im gleichseitigen Dreieck nicht angegeben werden. Dass du den hier verwendest bewirkt dann die wirkliche Verwirrung.

---

Dann wüsste ich gerne, wie man z ohne Pythagoras findet.

---

hallo,

ich habe dich Roland verstanden

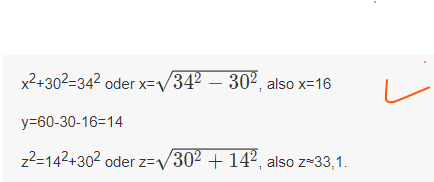
Text erkannt:

\( x^{2}+30^{2}=34^{2} \) oder \( x=\sqrt{34^{2}-30^{2}} \), also \( x=16 \)
\( y=60-30-16=14 \)
\( z^{2}=14^{2}+30^{2} \) oder \( z=\sqrt{30^{2}+14^{2}} \), also \( z \approx 33,1 \).

Also 60 * 33,1 ( Höhe) =1986 cm^2

andere 60 * 34 = 2040 cm^2

ABER was ist de Sinn , dss das Buch diesem Körper unterschiedliche Höhe ( 33,1 und 34 ) gibt?

also diene Methode stimmt mit dem Buch

30 * 60 ( unten) + 60 *33,1 ( links) + 60 *34 ( rechts) + 2 [  (30+60)/2 *30 ]= 85,26 cm^2 genau wie im Buch

---

ABER was ist de Sinn , dss das Buch diesem Körper unterschiedliche Höhe ( 33,1 und 34 ) gibt?

Deine Frage ist berechtigt.

Für mich ist klar, dass der Körper symmetrisch ist, die Trapeze eine Höhe von 30cm haben und die beiden Seiten der Trapeze jeweils 34cm lang sind und nur die Bemaßung der Höhe nicht optimal ist.

Wenn mit 30cm die Seitenlänge gemeint wäre,  dann wäre die Bemaßung genauso erfolgt, wie bei den 34cm.

Die angegebenen Lösungen sind also richtig.

---

Thanks a lot