stimmt das ?
nicht ganz.
Achte bitte arauf, dass Du Punkte und Seiten nicht verwechselst. Die Punkte werden mit großen und die Seiten mit kleinen Buchstaben bezeichnet.
1) gerade zweichnen( Siet C unten)
2) winkel in B mit Beta 112 eintarge
3)Kries um B mit a=3,8 schnedet in c
4) Um c Kries mit wy = 4,9 scheidet in D
besser:
1) gerade zeichnen( Seite c unten)
2) winkel in B mit Beta 112 eintragen
3) Kreis um B mit a=3,8 schnedet in C
4) Um C Kreis mit wy = 4,9 scheidet in D
4)Kries um M um denwinkle zu verdopllen dann bekomme A.
Das ist falsch, da der Punkt \(M\) noch gar nicht konstruiert wurde. Und es gibt auch keinen Hinweis in Deiner Beschreibung, was \(M\) sein soll.
Folgendes Vorgehen wäre relativ einfach:
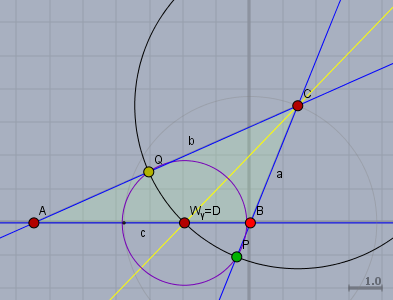
Wenn Du den Kreis (schwarz) um den Punkt \(C\) gezeichnest hast, so schneidet dieser nicht nur die Seite \(c\) in \(D\) (alias \(W_{\gamma}\)) sondern auch die Verlängerung der Seite \(a\) in \(P\) (grün). Nun brauchst Du nur einen Kreis (lila) um \(D\), durch \(P\), zu zeichnen, der den schwarzen Kreis in \(Q\) (gelb) schneidet.
Die Gerade durch \(C\) und \(Q\) ist das Spiegelbild zu \(a\).