Bestimme die Gleichung der Mittelsenkrechten der Strecke (AB) wenn, A(3,-5) B(2,-1)
Mittelpunkt der Strecke AB ist M((3+2)/2 | (-5-1)/2) = M(2.5 | -3)
Steigung der Geraden zwischen A und B ist
m = (-5 - (-1)) / (3 - 2) = -4
Senkrecht zur Steigung m ist die Steigung n = -1/(-4) = 1/4
Jetzt die Mittelsenkrechte in der Punkt-Steigungsform notieren
g(x) = n * (x - Mx) + My = 1/4 * (x - 2.5) - 3
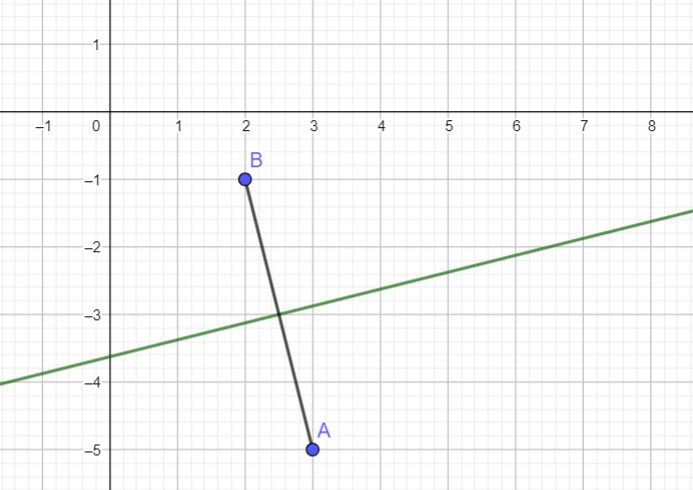
Skizze