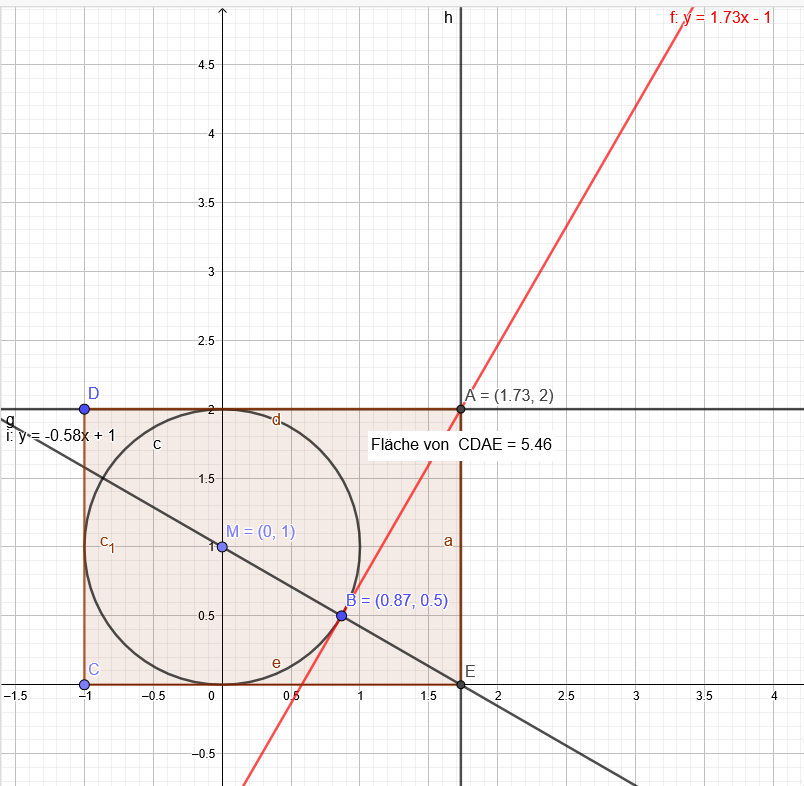
Gerade durch M(0|1)
tan (150°)=-\( \frac{1}{3} \)*\( \sqrt{3} \)
\( \frac{y-1}{x} \)=-\( \frac{1}{3} \)*\( \sqrt{3} \)
y=-\( \frac{1}{3} \)*\( \sqrt{3} \)*x+1
Schnitt mit Einheitskreis x^2+(y-1)^2=1
x^2+(-\( \frac{1}{3} \)*\( \sqrt{3} \)*x+1-1)^2=1
x^2+(-\( \frac{1}{3} \)*\( \sqrt{3} \)*x)^2=1
\( \frac{4}{3} \)x^2=1
Berührpunkt mit gleichseitigem Dreieck:
x=\( \frac{1}{2} \)\( \sqrt{3} \) y=-\( \frac{1}{3} \)*\( \sqrt{3} \)*\( \frac{1}{2} \)\( \sqrt{3} \) +1=\( \frac{1}{2} \)
Tangente an Einheitskreis:
tan(60°)=\( \sqrt{3} \)

\( \begin{array}{l} y-\frac{1}{2} \\ {x-\frac{1}{2} \cdot \sqrt{3}}=\sqrt{3} \\ y=\sqrt{3} \cdot\left(x-\frac{1}{2} \cdot \sqrt{3}\right)+\frac{1}{2} \end{array} \)
\( y=\sqrt{3} \cdot x-1 \)
Schnitt mit \( y=2 \) (obere Begrenzung Rechteck)
\( \begin{array}{l} 2=\sqrt{3} \cdot x-1 \\ \sqrt{3} \cdot x=3 \\ x=\frac{3}{\sqrt{3}}=\sqrt{3} \end{array} \)
Die halbe Rechteckfläche:
Linke Kreisbegrenzung \( x=-1 \)
\( A_{\frac{1}{2}}=(1+\sqrt{3}) \cdot 2=2+2 \cdot \sqrt{3} \)
\( A=4+4 \cdot \sqrt{3} \)