Hallo, wie oben schon geschrieben würde ich gerne erfragen ob meine beiden geraden Gleichungen richtig bestimmt sind?
Vielleicht kann ja dann noch geguckt werden ob ich im weiteren Verlauf richtig gerechnet habe? Zumindest der Rechenweg der richtige ist.
Aufgabe:
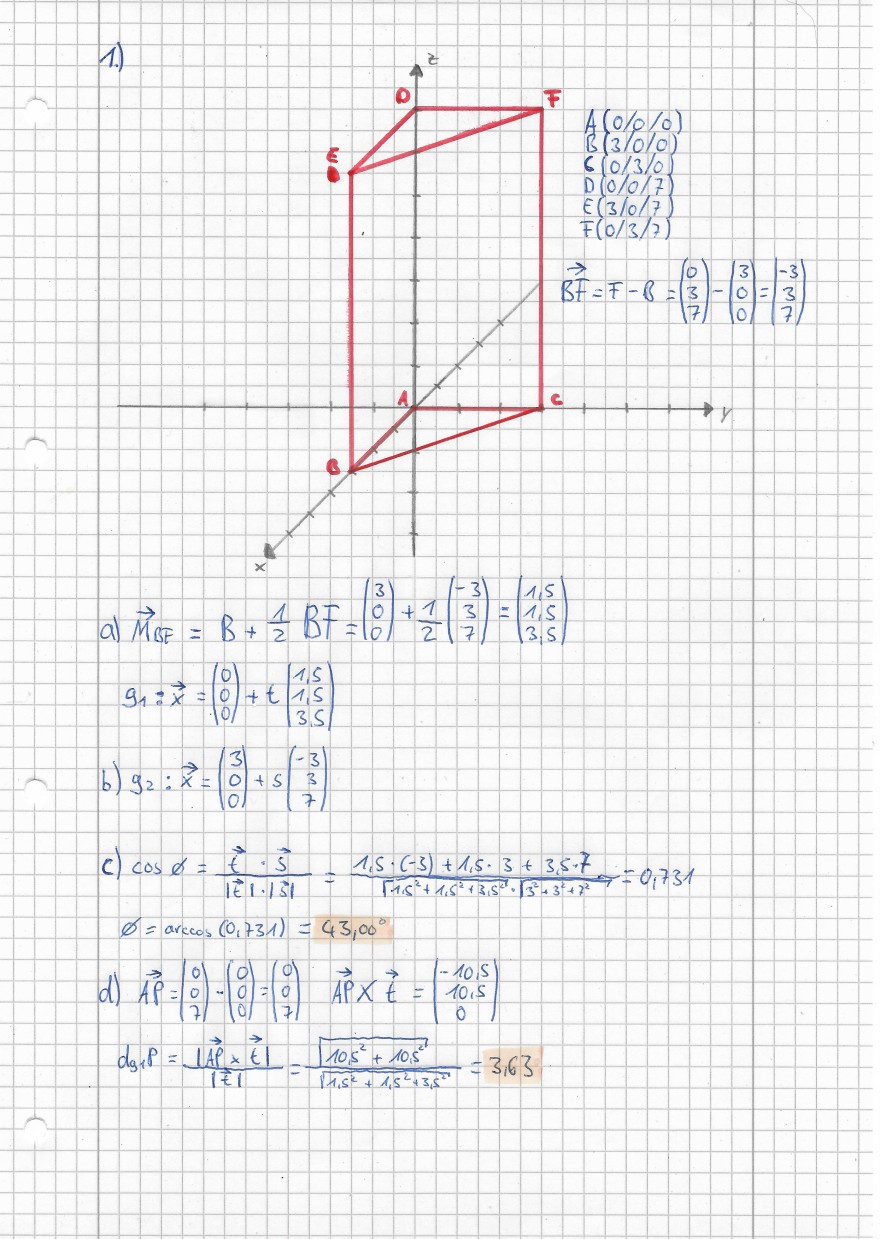
1. Gegebene sei ein gerades Dreiecksprisma ABC DEF der Höhe \( 7 \mathrm{~cm} \). Die Grundseite ABC sei gleichschenklig \( (\overline{A B}=\overline{A C}=3 \mathrm{~cm}) \) und rechtwinklig. Der Punkt A liege im Ursprung A=O und die Punkte B und C liegen auf der \( \mathrm{x}- \) bzw. der \( \mathrm{y} \) - Achse. Eine Gerade \( g_{1} \) enthalte den Punkt am rechten Winkel der Grundseite und den Mittelpunkt der gegenüberliegenden rechteckigen Seitenfläche des Prismas.(a) Geben Sie eine Gleichung der Geraden \( g_{1} \) an. ( \( 1 \mathrm{BE} \) )(b) Geben Sie eine Gleichung der Geraden \( g_{2} \) an, die die Flächendiagonale \( \overline{B F} \) enthält. (1 BE)(c) Berechnen Sie den Schnittwinkel zwischen \( g_{1} \) und \( g_{2} .(2 \mathrm{BE}) \)(d) Berechnen Sie den Abstand der Geraden \( g_{1} \) vom Punkt D. (2 BE)(e) Untersuchen Sie, ob sich die Gerade \( g_{1} \) und die Gerade \(g_{3}\) (1\0\1)+s(2\1\2)schneiden. Gegeben Sie gegebenenfalls den Schnittpunkt an. (2 BE).(f) Geben Sie den Punkt E in der Basis mit den Basisvektoren \( \vec{B}, \vec{C}, \vec{D} \) an. \( (1 \mathrm{BE}) \)(g) Drehen Sie das Prisma um \( 45^{\prime} \) um die z-Achse.
Lösungen