Hallo Roland,
ich verzichte mal darauf zu zeigen, dass es sich beim Viereck \(EPBQ\) um ein Quadrat handelt; das ist einfach. Da alle bunt marklierten Strecken gleich lang sind, ist außerdem \(|AD|=|GP|\). Es sei$$|FE| = |AD| = a, \quad |FQ|=|XB|=b, \quad |BP|=c$$
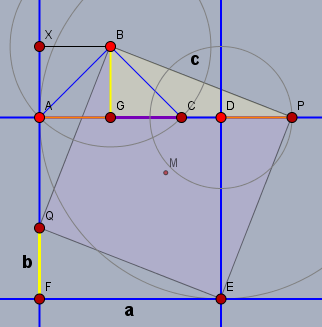
dann muss man nur noch die Flächen zusammen zählen, aus denen sich das Quadrat \(EPBQ\) mit der Kantenlänge \(c\) zusammen setzt:$$\begin{aligned} c^2&=a^2\underbrace{-F_{\triangle FEQ} + F_{\triangle EPD}}_{=0} - \underbrace{F_{QBX}}_{=\frac 12ab} + \underbrace{F_{AGBX}}_{=b^2}+\underbrace{F_{\triangle BGP}}_{=\frac 12ab} \\&= a^2+b^2 \end{aligned}$$Gruß Werner