Bestimme die Definitions- und die Wertemenge der Funktion f mit f(x)=\frac{2}{x-3}-4

Question

Aufgabe:

Kann mir jemand bei dieser Aufgabe helfen?

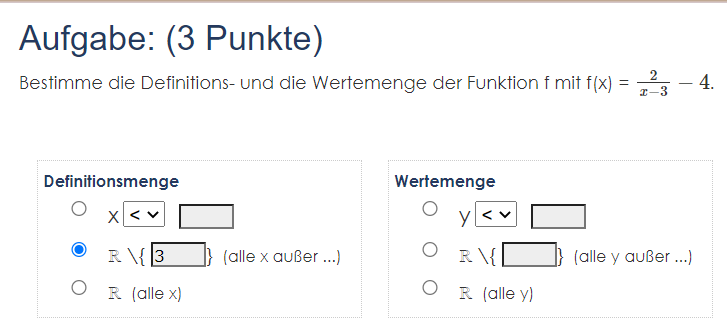
Text erkannt:

Aufgabe: \( { }^{\prime} \) P unkte)
Bestimme die Definitions- und die Wertemenge der Funktion \( f \) mit \( f(x)=\frac{2}{x-3}-4 \)
Definitionsmenge
Wertemenge
\( y<v \)
\( \mathbb{R} \backslash\{3\} \) (alle x außer ...)
\( \mathbb{R} \backslash\{\square \quad\} \quad \) (alle y außer ...)
\( R \) (alle \( x \) )
\( R \) (alle y)

Comments

Also so ?

Text erkannt:

Aufgabe: (3 Punkte)
Bestimme die Definitions- und die Wertemenge der Funktion f mit \( \mathrm{f}(\mathrm{x})=\frac{2}{x-3}-4 \).
Definitionsmenge
\( \begin{array}{c}\text { Wertemenge } \\ \text { x }<v\end{array} \)
\( \mathbb{R} \backslash\{3\} \) (alle x auber ...)
\( \mathbb{R} \backslash\left\{\begin{array}{lll}-4 & \text { (alle y auber ...) }\end{array}\right. \)
\( \mathbb{R} \) (alle \( x \) )
\( \mathbb{R} \) (alle y)

Answer 1

Def.menge ist richtig. Wertemenge: alles ohne -4.

Answer 2

2 / ( x - 3 ) - 4

In der Def-Menge muß eine Division durch null ausgeschlossen werden.

x - 3 = 3
x = 3

D = R ohne die 3
y = 2 / ( x - 3 ) -4
Umkehrfunktion
x = 2 / ( y - 3 ) -4
x + 4 = 2 / ( y - 3 )
y + 3 = 2 / ( x + 4 )
y =  2 / ( x + 4 ) - 3
D = R ohne die -4

W der Funktion ist gleich D der Umkehrfunktion

W = R ohne die -4

Comments

Also so ?

Text erkannt:

Aufgabe: (3 Punkte)
Bestimme die Definitions- und die Wertemenge der Funktion f mit \( \mathrm{f}(\mathrm{x})=\frac{2}{x-3}-4 \).
Definitionsmenge
\( \begin{array}{c}\text { Wertemenge } \\ \text { x }<v\end{array} \)
\( \mathbb{R} \backslash\{3\} \) (alle x auber ...)
\( \mathbb{R} \backslash\left\{\begin{array}{lll}-4 & \text { (alle y auber ...) }\end{array}\right. \)
\( \mathbb{R} \) (alle \( x \) )
\( \mathbb{R} \) (alle y)

---

Die angeklickten Lösungen scheinen
meiner Lösung zu entsprechen.

---

D = R ohne die -4

Viel Spaß, wenn hj2166 kommt. Er hat heute noch niemanden ans Bein gepisst.
Die Schreibweise ist eigentlich ein Hinrichtungsgrund für unseren Scharfrichter. :)))