Question

Aufgabe:Kann man Faktoren bei Funktionsuntersuchungen ausschließen?

Problem/Ansatz:Hallo, ich habe mal eine Frage bezüglich Faktoren. Bei Funktionenschar fk(x)=1/k(kx^2-2x) muss ich beispielsweise Nullstellen und Extrempunkte durch Ableitungen berechnen. In der Lösung haben die das 1/k einfach ignoriert beim Null setzten und ableiten aber bei der Ableitung davor geschrieben. Darf ich das einfach so? Und musst ich dann auf was besonderes achten?

Vielen Dank im Voraus

Answer 1

fk(x)=\( \frac{1}{k} \)* (kx^2-2x)

Nullstellen:

\( \frac{1}{k} \)* (k*x^2-2x)=0|*k

k*x^2-2x=0

x*(k x-2)=0

x₁=0

x₂=\( \frac{2}{k} \)

Extrema:

f´(x)=\( \frac{1}{k} \)* (2kx-2)

\( \frac{1}{k} \)* (2kx-2)=0|*k

2kx-2=0

x₁=\( \frac{1}{k} \)   y₁=\( \frac{1}{k} \)* (k*\( \frac{1}{k} \) ^2-2*\( \frac{1}{k} \) )

Betreffendes \( \frac{1}{k} \) benötigst du damit nur bei der Berechnung des Funktionswertes.

Art des Extremwertes:

f´´(x)=\( \frac{1}{k} \)* (2k)=2>0 Minimum

Hier ist es dann auch wieder nötig.

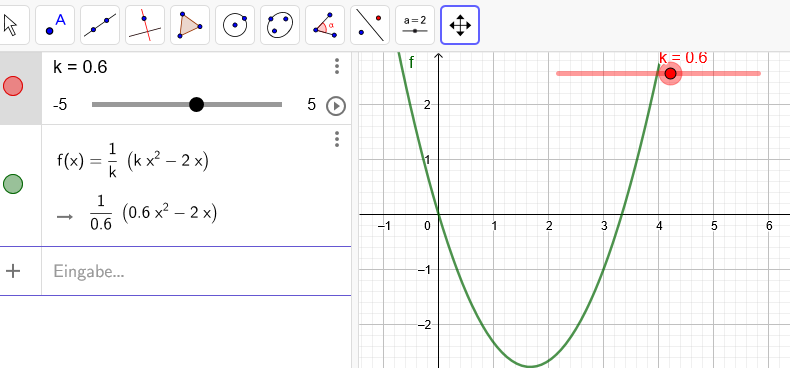
Text erkannt:

A
k \( =0.6 \)
\( -5 \)
\( f(x)=\frac{1}{k}\left(k x^{2}-2 x\right) \)
\( \rightarrow \frac{1}{0.6}\left(0.6 x^{2}-2 x\right) \)
Eingabe...