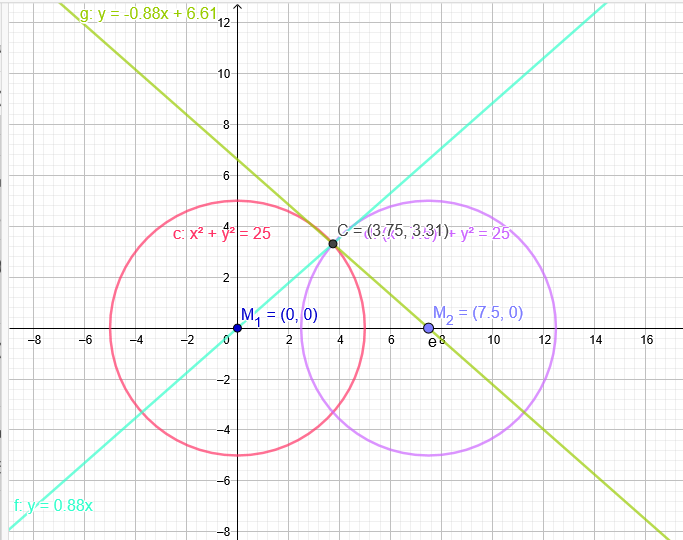
Beide Kreise haben jeweils einen Radius von r= 5cm. Die Entfernung der Mittelpunkte M1 und M2 der beiden Kreise beträgt 1,5r.
a) Zeichne die beiden Kreise
b) Berechne das Maß γ des Winkels M₁C M₂.
Koordinaten von C:
Kreis um M₁(0|0) mit r=5
1.)x^2+y^2=25
Kreis um M₂(5*1,5|0) mit r=5
2.) (x-7,5)^2+y^2=25
1.)-2.) x^2- (x-7,5)^2=0 → x=3,75 1.) 3,75^2+y^2=25 y=+-3,31 Ich rechne mit dem +Wert weiter
C(3,75|3,31)
Geradensteigung der Geraden durch M₁(0|0) und C(3,75|3,31)
m₁=\( \frac{3,31}{3,75} \)=0,88
Geradensteigung der Geraden durch M₂(5*1,5|0) und C(3,75|3,31)
m₂=\( \frac{3,31-0}{3,75-7,5} \)=-0,88
Winkel bei C
tanγ=|\( \frac{m₂-m₁}{1+m₁*m₂} \)|
tanγ=|\( \frac{-0,88-0,88}{1+0,88*(-0,88)} \)|=|-7,8|=7,8
\( tan^{-1} \)(7,8)=1,443287
γ=82,69°
c) Berechne die Länge CA. Wo liegt A?