Aufgabe:
Bestimme die punktuelle Steigung bei \( x=-2,5 \), indem du eine Tangente dort einzeichnest und ihre Steigung bestimmst.
Problem/Ansatz: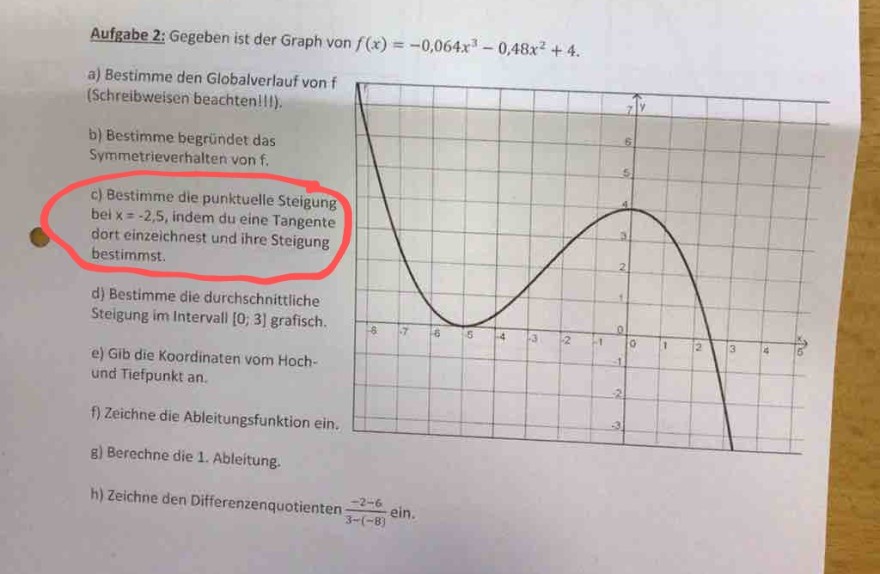
Text erkannt:
Aufgabe 2: Gegeben ist der Graph von \( f(x)=-0,064 x^{3}-0,48 x^{2}+4 \)
a) Bestimme den Globalverlauf von \( f \)
(Schreibweisen beachten!ll).
b) Bestimme begründet das
Symmetrieverhalten von f. d) Bestimme die durchschnittliche Steigung im Intervall \( [0 ; 3] \) grafisch. e) Gib die Koordinaten vom Hoch- und Tiefpunkt an.
bei \( x=-2,5 \), indem du eine Tangente dort einzeichnest und ihre Steigungente bestimmst.
f) Zeichne die Ableitungsfunktion ein.
g) Berechne die 1. Ableitung.
h) Zeichne den Differenzenquotienten \( \frac{-2-6}{3-(-83} \) ein.
Ich muss die Aufgabe ohne GTR und ohne Steigungsdreieck rechnen.
Dies ist keine Buchseite, sondern ein zur Verfügung gestelltes Arbeitsblatt