 Vermutlich so:
Vermutlich so:
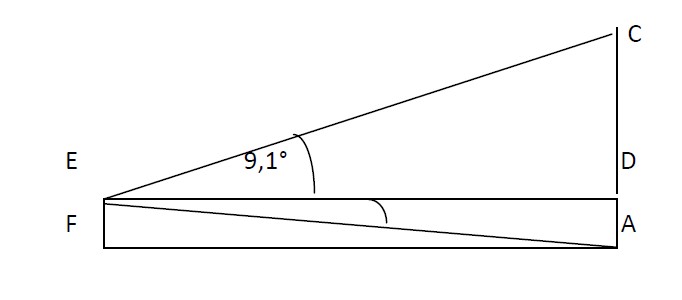
Dreieck EFA hat bei F einen rechten Winkel, bei E einen
Innenwinkel von 89,4° und bei A einen von 0,6° .
Die Kathete EF = 157 cm = 1,57m
Und ED ist die Parallele zum Boden (FA) durch die
Spitze des Messgerätes. Dann gilt
tan(0,6°) = 1,57m / FA
==> FA = 1,57m / tan(0,6°) = 1,57m / 0,0105 =149,5m
Und wegen ED = FA gilt im Dreieck EDC
tan(9,1°) = CD/ ED = CD / 149,5m
==> CD = 149,5m * tan(9,1°) = 149,5m *0,1602 =23,95m
Und weil EF = AD ist, also AC=AD+CD
= 1,57m+23,95m=25,52m.
Das sit die Höhe des Leuchtturms.