Wie tief ist der Kanal?

Question

Aufgabe:

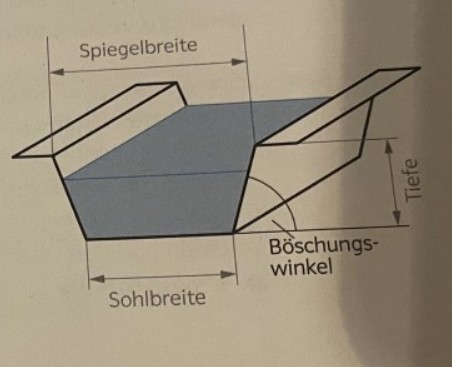
Der Querschnitt eines Kanals ist ein gleichschenkeliges Trapez \( (a \| c, b=d) \) mit folgenden Abmessungen: Sohlbreite \( a=22,0 \mathrm{~m} \), Spiegelbreite \( c=65,0 \mathrm{~m} \), Böschungswinkel \( \gamma=40^{\circ} \).

1) Wie tief ist der Kanal?

Problem/Ansatz:

Answer 1

Strecke H_c C=\( \frac{65-22}{2} \)=21,5

tan(50°)=\( \frac{21,5}{h_c} \)

Querschnittsfläche:\( \frac{a+c}{2} \)•h_c

A=\( \frac{22+65}{2} \)•h_c

Volumen: A*300

Comments

Was ist hier jetzt hc ?

---

hc ist die gesuchte Tiefe des Kanals.

Ich habe eine Skizze eingefügt:

---

Eine letzte Frage wie komme ich auf 50 grad

---

Summe der Innenwinkel eines Dreiecks = 180°

180 - 90 - 40 = 50

Answer 2

Hallo,

das Dreieck BPC ist rechtwinklig.

Jetzt solltest du die Tiefe h, die du auch zu Berechnung des Flächeninhaltes brauchst, berechnen können.

Sonst melde dich nochmal.

Gruß, Silvia