Aufgabe:
Seien k, n ∈ N0 mit 0 ≤ k ≤ n. Beweisen Sie die folgende Aussage ohnevbinomischen Lehrsatz zu verwenden:
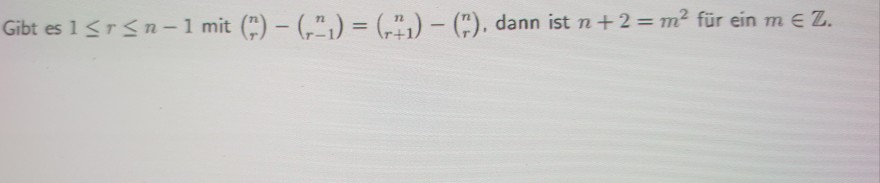
Text erkannt:
Gibt es \( 1 \leq r \leq n-1 \) mit \( \left(\begin{array}{l}n \\ r\end{array}\right)-\left(\begin{array}{c}n \\ r-1\end{array}\right)=\left(\begin{array}{c}n \\ r+1\end{array}\right)-\left(\begin{array}{l}n \\ r\end{array}\right) \), dann ist \( n+2=m^{2} \) für ein \( m \in \mathbb{Z} \).
Problem/Ansatz:
Ich bin seit 4 Stunden mit dieser Aufgabe dabei aber ich kriege es nicht hin. Ich möchte einfach weinen. Bitte helfen Sie mir! Das bedeutet viel für mich.