Hallo,
Willkommen in der Mathelounge!
Zeichne zunächst eine Gerade und trage dort die Strecke \(|AB|=6\,\text{cm}\) ab, Der Thaleskreis (grün) über \(AB\) schneidet den Kreis um \(B\) mit dem Radius \(h_B = 3,5\,\text{cm}\) oberhalb der Geraden in \(H_b\). Die Seite \(b\) liegt auf der Geraden durch \(AH_b\).
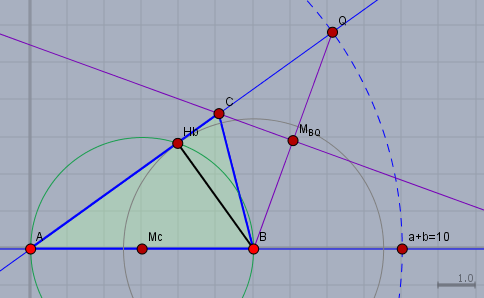
Bis hierhin solltest Du selbst gekommen sein. Nun kommt die Sache mit \(a+b=10\,\text{cm}\).
Trage diese \(10\,\text{cm}\) auf der Geraden durch \(AH_b\) ab; so erhältst Du den Punkt \(Q\). Konstruiere nun die Mittelsenkrechte über der Strecke \(BQ\) (beide lila). Diese Mittelsenkrechte schneidet die Gerade durch \(AH_b\) im Punkt \(C\).
Offensichtlich ist \(|CQ| = |CB| = a\) und somit \(a+b=10\,\text{cm}\). Sollte noch etwas unklar sein, so frage bitte nach.
Gruß Werner