Kurven modellieren Kurvendiskussion

Question

Aufgabe:

Ich brauche eine Hilfe bitte :)

Die Aufgabe lautet:

Eine Polynomfunktion 3. Grades geht durch den Koordinatenursprung und hat dort den Anstieg -4. Im Punkt P(2|-8)

ist ein lokales Minimum.

Ich habe bis jetzt:

f(x):= ax³+bx²+cx+d

f(-4)=0

Problem/Ansatz:

Ich verstehe diese mit lokales Minimum nicht ganz?

Heißt es :

f'(2)=0 oder f'(2)=-8

Answer 1

Hallo,

ein Minimum in dem Punkt bedeutet

\(f(2)=-8\\ f'(2)=0\)

Gruß, Silvia

Answer 2

Aloha :)

Die Gesuchte ist eine Polynomfunktion 3-ten Grades:$$f(x)=ax^3+bx^2+cx+d$$$$f'(x)=3ax^2+2bx+c$$Sie geht durch den Koordinatenursprung:$$0\stackrel!=f(0)=a\cdot0+b\cdot0+c\cdot0+d=0\implies d=0$$Im Urpsrung hat sie den Anstieg \((-4)\):$$-4\stackrel!=f'(0)=3a\cdot0+2b\cdot0+c\implies c=-4$$Der Punkt \((2|-8)\) liegt auf ihrem Graphen. Mit \(c=-4\) und \(d=0\) heißt das:$$-8\stackrel!=f(2)=a\cdot8+b\cdot4-4\cdot2=8a+4b-8\implies8a+4b=0\implies2a+b=0$$Im Punkt \((2|-8)\) hat die Gesuchte ein lokales Minimum. Mit \(c=-4\) heißt das:$$0\stackrel!=f'(2)=3a\cdot4+2b\cdot2-4=12a+4b-4\implies12a+4b=4\implies 3a+b=1$$Wegen \(2a+b=0\) und \(3a+b=1\) folgt sofort:$$1=3a+b=a+(2a+b)=a+0\implies a=1$$Schließlich folgt aus \(2a+b=0\) und \(a=1\):$$b=-2a=-2\cdot1=-2$$Damit haben wir die Gesuchte gefunden:$$f(x)=x^3-2x^2-4x$$

~plot~ x^3-2x^2-4x ; {0|0} ; {2|-8} ; -4x ; [[-4|5|-9|4]]  ~plot~

Comments

Danke dir, sehr hilfreich :)

Answer 3

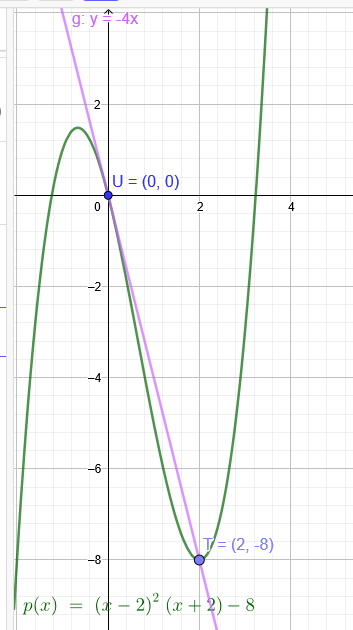
"Eine Polynomfunktion 3. Grades geht durch den Koordinatenursprung U(0|0)und hat dort den Anstieg -4. Im Punkt T(2|-8) ist ein lokales Minimum."

Lösungsmöglichkeit (Problem/Ansatz ist schon beantwortet.):

Ich verschiebe den Graphen um 8 Einheiten nach oben:

T´(2|0)  lokales Minimum

f(x)=a*(x-2)^2*(x-N)

U´(0|8)

f(0)=a*(0-2)^2*(0-N)      1.) -4aN=8     a=-\( \frac{2}{N} \)

f(x)=-\( \frac{2}{N} \)*[(x-2)^2*(x-N)]

Anstieg in  U´   m=-4

f´(x)=-\( \frac{2}{N} \)*[(2x-4)*(x-N)+(x-2)^2]

f´(0)=-\( \frac{2}{N} \)*[(-4)*(-N)+4]

-\( \frac{2}{N} \)*[(-4)*(-N)+4]=-4       N=-2     a=1

f(x)=[(x-2)^2*(x-(-2)]= (x-2)^2*(x+2)

Wieder 8 Einheiten nach unten verschieben:

p(x)= (x-2)^2*(x+2)-8