Unbegrenzte/begrenzte Flächen?

Question

Aufgabe:

Gegeben sind die Funktionen f mit:

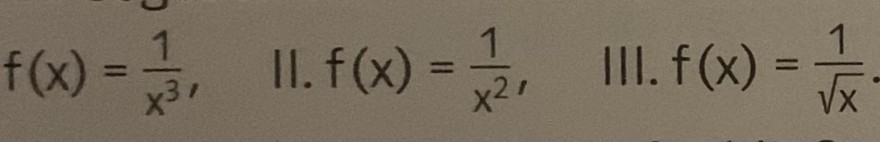
Text erkannt:

\( f(x)=\frac{1}{x^{3}}, \quad\left\|. f(x)=\frac{1}{x^{2}}, \quad\right\| 11 . f(x)=\frac{1}{\sqrt{x}} \)

a) Der Graph jeder Funktion f schließt mit der x-Achse für x ≥ 1 eine nach rechts unbegrenzte
Fläche ein. Untersuchen Sie, ob diese Fläche einen endlichen Inhalt hat.
b) Untersuchen Sie entsprechend die nach oben unbegrenzte Fläche.

Problem/Ansatz:

Verstehe ich nicht- bitte Schritt für Schritt erklären!

Answer 1

a) Der Graph jeder Funktion f schließt mit der x-Achse für x ≥ 1 eine nach rechts unbegrenzte Fläche ein. Untersuchen Sie, ob diese Fläche einen endlichen Inhalt hat.

∫ (1 bis ∞) (1/x^3) dx = 1/2
∫ (1 bis ∞) (1/x^2) dx = 1
∫ (1 bis ∞) (1/√x) dx = ∞

Answer 2

Beispielhaft
f = 1/x^3
Stammfunktion
S = -1 / (2x^2)
S zwischen 1 bis ∞ ( Einsetzen )
-1 / (2 * (∞) ^2)  minus -1 / (2 * (1)^2)
0 + 1 / 2
1 / 2
Frag´ nach bis alles klar ist.

Schau nach bei " uneigentliche Integrale "