Aufgabe:
Der Körper \(K ⊆ \mathbb R^3\) sei durch die Flächen \(z= \sqrt{x^2+y^2} \) und \(z = \sqrt{1-x^2-y^2}\) begrenzt. Stellen Sie \(K\) als Normalbereich dar, und zwar in
(a) kartesischen Koordinaten
(b) Zylinderkoordinaten
Problem/Ansatz:
Also der "Körper" hier Dunkelblau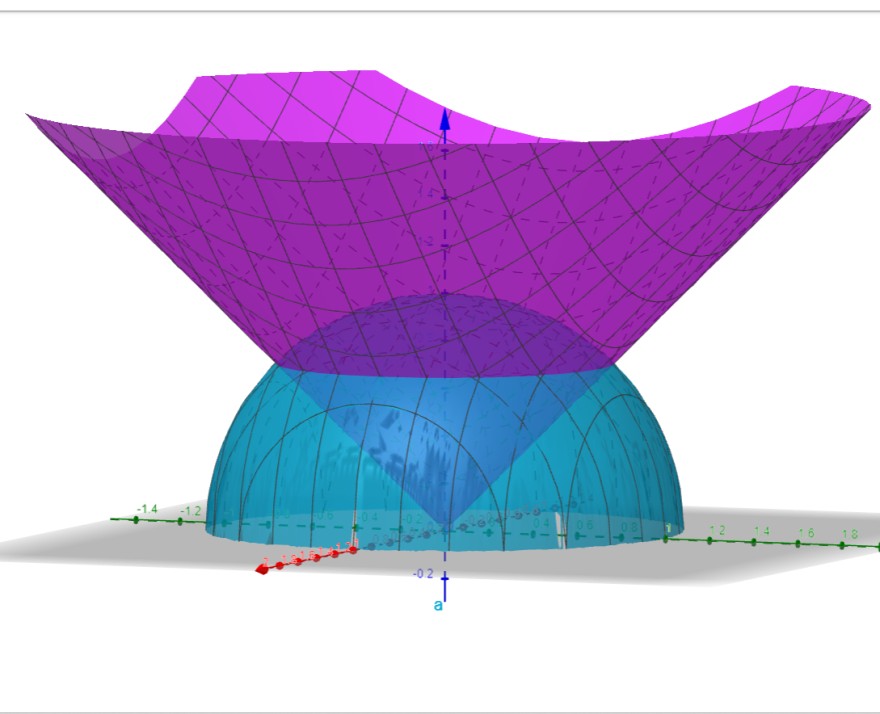 Ich habe extreme Schwierigkeiten mit der Aufgabe. Kann mir jemand vielleicht seine Herangehensweise erläutern? Das wäre sehr hilfreich.
Ich habe extreme Schwierigkeiten mit der Aufgabe. Kann mir jemand vielleicht seine Herangehensweise erläutern? Das wäre sehr hilfreich.