Bestimmen Sie alle Stellen, an denen g(x)=3 \lfloor x \rfloor^3 stetig ist mit Begründung

Question

Ich habe eine Aufgabe, bei der ich einfach nicht weiterkomme:

Sei \( g: \mathbb{R} \rightarrow \mathbb{R} \) gegeben durch
\(g(x)=3 \lfloor x \rfloor^3 \) für alle \( x \in \mathbb{R} \).

Bestimmen Sie alle Stellen, an denen g stetig ist. Begründen Sie dabei Ihre Behauptungen.

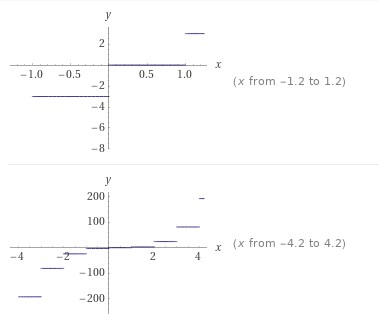
Aus dem Bild kann man erkennen, dass die Funktion nicht auf dem gesamten R stetig ist, sondern nur auf diesen einzelnen horizontalen Stellen.
Wenn meine Intuition richtig ist, müsste diese Funktion an allen Punkten \(a \in \mathbb{R} \setminus \mathbb{Z}\) stetig sein und an den Punkten \(a \in \mathbb{Z}\) unstetig.

Aber wie kann ich nun diese beiden Fälle zeigen?

Answer 1

Hallo

da die funktion an allen nicht ganzen Stellen konstant ist  und f(x)=const stetig ist muss du nur zeigen dass der rechtzeitige und linksseitige Grenzwert gegen x in ℤ nicht gleich ist also an den Stellen unstetig, für nicht ganze Stellen sind die GW gleich.

lul