1 Gegeben sind folgende Funktionen:
f mit \( f(x)=-x^{4} ; g \) mit \( g(x)=x^{9} ; \) h mit \( h(x)=-x^{5} \)
Bestimmen Sie die Funktionen darunter, deren Schaubilder
a) achsensymmetrisch zur \( y \)-Achse sind.
b) den IV. Quadranten durchlaufen.
c) den Punkt \( P(1 \mid 1) \) enthalten.
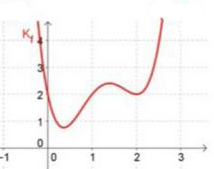
2 Bestimmen Sie die Funktionsterme zu den Schaubildern \( K_{f} \) und \( K_{g} \).

3 Bestimmen Sie den globalen Verlauf, die Schnittpunkte mit den Koordinatenachsen sowie die Vielfachheit der Nullstellen und skizzieren Sie anschließend den Verlauf der Schaubilder für die folgenden Funktionen:
a) \( f(x)=-x^{2}(x-2)^{2} \)
b) \( h(x)=0,5 x^{3}-4 \)
c) \( g(x)=x^{4}-4 x^{2}+4 \)
4 Wahr oder falsch? Begründen Sie:
a) Das Schaubild einer Polynomfunktion 5. Grades kann nicht mehr als zwei doppelte Nullstellen besitzen.
b) Zwei Polynomfunktionen mit unterschiedlichem Grad haben außer dem Ursprung nur einen weiteren Schnittpunkt.
c) Wenn \( f(x) \) und \( g(x) \) Polynomfunktionen mit geradem Grad sind, so ist auch \( h(x)=f(x)+g(x) \) eine Polynomfunktion mit geradem Grad.
d) Wenn \( f(x) \) und \( g(x) \) Polynomfunktionen mit geradem Grad sind, so ist auch \( h(x)=f(x)-g(x) \) eine Polynomfunktion mit geradem Grad.
5 Stellen Sie einen Funktionsterm zu folgendem Schaubild auf: