Grenzwerte berechnen (geometrische Folge)

Question

Aufgabe:

…

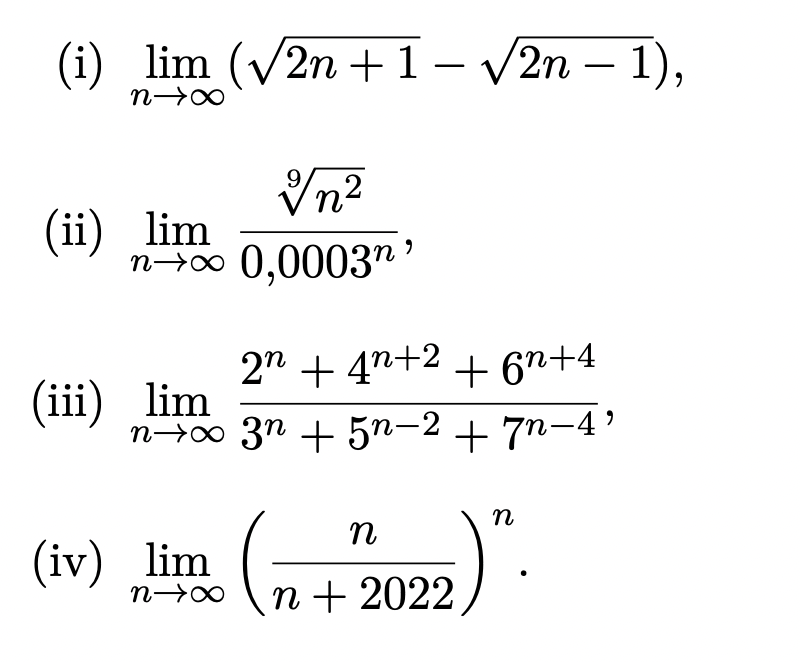
Text erkannt:

(i) \( \lim \limits_{n \rightarrow \infty}(\sqrt{2 n+1}-\sqrt{2 n-1}) \),
(ii) \( \lim \limits_{n \rightarrow \infty} \frac{\sqrt[9]{n^{2}}}{0,0003^{n}} \)
(iii) \( \lim \limits_{n \rightarrow \infty} \frac{2^{n}+4^{n+2}+6^{n+4}}{3^{n}+5^{n-2}+7^{n-4}} \),
(iv) \( \lim \limits_{n \rightarrow \infty}\left(\frac{n}{n+2022}\right)^{n} \).

Problem/Ansatz:

Answer 1

1. Erweitere zur 3. binomischen Formel

2. 9-te Wurzel aus n^2 = n^(2/9)

3. Kürze mit 7^n

4. n/(n+2022) = (n+2022-2022)/(n+2022) = 1- 2022/(n+2022)

Comments

Was sollte man aus der letzten Umformung schließen?

---

Noch als Tipp u= -(n+2020)/2020

und dann sollte er es lösen können

---

Wie kommt man bei der (i) auf die Herleitung zur dritten binomischen Formel

---

Weil man so die Wurzel im entstehenden Zähler wegbekommt und das n dort verschwindet, wenn man zusammenfasst.

---

Habs versucht zu rechnen aber ich komme leider einfach nicht drauf , Wäre es möglich wenn du es vorrechnest ?

---

weil a^2 ist ja dann Wurzel aus 2n+1 und b^2 ist dann Wurzel aus 2n-1. Also ist a die Wurzel der Wurzel aus 2n+1 usw

---

Wäre es möglich wenn du es vorrechnest ?

... ganz im Detail:$$\phantom=\lim \limits_{n \to \infty}(\sqrt{2 n+1}-\sqrt{2 n-1})\\ = \lim\limits_{n \to \infty}\frac{\sqrt{2 n+1}-\sqrt{2 n-1}}{1}\\ = \lim\limits_{n \to \infty}\frac{(\sqrt{2 n+1}-\sqrt{2 n-1})\cdot (\sqrt{2n+1}+\sqrt{2n-1})}{1\cdot (\sqrt{2n+1}+\sqrt{2n-1})}\\ = \lim\limits_{n \to \infty}\frac{(\sqrt{2 n+1})^2-(\sqrt{2 n-1})^2}{\sqrt{2n+1}+\sqrt{2n-1}}\\ = \lim\limits_{n \to \infty}\frac{(2n+1)-(2n-1)}{\sqrt{2n+1}+\sqrt{2n-1}}\\ = \lim\limits_{n \to \infty}\frac{2n+1-2n+1}{\sqrt{2n+1}+\sqrt{2n-1}}\\ = \lim\limits_{n \to \infty}\frac{2}{\sqrt{2n+1}+\sqrt{2n-1}}\\ = 0 \quad \text{da}\space \lim\limits_{n \to \infty}(\sqrt{2n+1}+\sqrt{2n-1}) \to \infty$$

---

Zähler: 2n+1 -(2n-1) = 2
Nenner:  √(2n+1) +√(2n-1)

Nenner geht gegen oo für n gegen oo -> lim = 2/oo = 0
 

---

xxxxxxxxxxxxxxx

---

Kannst du bei der (iii) erklären wie du mit 7^n kürzt ?

---

Kannst du bei der (iii) erklären wie du mit 7ⁿ kürzt ?

$$\phantom=\lim \limits_{n \to\infty} \frac{2^{n}+4^{n+2}+6^{n+4}}{3^{n}+5^{n-2}+7^{n-4}} \\ = \lim \limits_{n \to\infty} \frac{\left(2^{n}+4^{n+2}+6^{n+4}\right)\div 7^n}{\left(3^{n}+5^{n-2}+7^{n-4}\right)\div 7^n} \\ = \lim \limits_{n \to\infty} \frac{\left(\frac{2}{7}\right)^n + 4^2\left(\frac{4}{7}\right)^n+6^4\left(\frac{6}{7}\right)^n}{\left(\frac{3}{7}\right)^n + 5^{-2}\left(\frac{5}{7}\right)^n+7^{-4}\underbrace{\left(\frac{7}{7}\right)^n}_{=1}}\\ = \frac{0+0+0}{0+0+7^{-4}} \\=0$$Jeder Term der Form \(q^n\) mit \(|q|<1\) geht mit \(n\to\infty\) gegen \(0\). Und da im Nenner ein endlicher Ausdruck \(7^{-4}\gt 0\) stehen bleibt, wird der gesamte Bruch zu \(0\).

Answer 2

I) dritte binomische Formel

(II) z.b. L'hopital

IV) sieht sehr stark nach ähnlichen Grenzwert der Zahl e aus, musste nur bisschen umformen und 0 Addition im Zähler dann kommste drauf

Comments

Bei der (iv) kommt 1/e^2022 raus aber ich verstehe nicht wie man drauf kommen soll, kannst du es mir vielleicht vorrechnen ?

---

Bei der (iv) kommt 1/e2022 raus aber ich verstehe nicht wie man drauf kommen soll, kannst du es mir vielleicht vorrechnen ?

Substituiere \(n=2022m\), dann sieht das so aus$$\phantom=\lim\limits_{n \rightarrow \infty}\left(\frac{n}{n+2022}\right)^{n} \quad\quad n=2022m \\ =\lim\limits_{m \rightarrow \infty}\left(\frac{2022m}{2022m+2022}\right)^{2022m} \\ = \lim\limits_{m\to\infty}\left(\left(\frac{m}{m+1}\right)^m\right)^{2022}\\ = \left(\frac1e\right)^{2022}$$und das gilt weil ...$$\frac1e=\frac1{\lim\limits_{n\to \infty}\left(1+\frac1n\right)^n} = \lim\limits_{n\to \infty} \frac1{\left(\frac{n+1}n\right)^n}=\lim\limits_{n\to \infty}\left(\frac{n}{n+1}\right)^n$$