Rekonstruktion einer Funktion des 4. Grades

Question

Aufgabe:

Der Graph einer ganz rationalen Funktion 4. Grades geht durch P(1;1) berührt die x-Achse im Ursprung und hat einen Sattelpunkt bei x=2

Problem/Ansatz:

f(x) = ax^4 + bx^3 + cx^2 +dx + e

zu den Eigenschaften:

f(0) = 1 ?

Answer 1

Aloha :)

Der Graph berührt die \(x\)-Achse im Ursprung, also muss bei \(x=0\) eine doppelte Nullstelle vorliegen, d.h. der Funktionsterm enhält den Faktor \(x^2\), daher hat die Funktionsgleichung die Form:$$f(x)=x^2(ax^2+bx+c)=ax^4+bx^3+cx^2$$Der Graph hat einen Sattelpunkt bei \(x=2\), also verschwinden dort die ersten beiden Ableitungen:$$f'(x)=4ax^3+3bx^2+2cx\quad\implies\quad 0\stackrel!=f'(2)=32a+12b+4c$$$$f''(x)=12ax^2+6bx+2c\quad\implies\quad 0\stackrel!=f''(2)=48a+12b+2c$$Der Punkt \((1|1)\) liegt auf dem Graphen:$$1=f(1)=a+b+c$$Damit haben wir folgendes Gleichungssystem:$$\begin{pmatrix}8 & 3 & 1\\24 & 6 & 1\\1 & 1 & 1\end{pmatrix}\begin{pmatrix}a\\b\\c\end{pmatrix}=\begin{pmatrix}0\\0\\1\end{pmatrix}$$Mit der Lösung:$$a=\frac{3}{11}\quad;\quad b=-\frac{16}{11}\quad;\quad c=\frac{24}{11}$$

Der gesuchte Funktionsterm lauet daher:$$f(x)=\frac{1}{11}\left(3x^4-16x^3+24x^2\right)$$

~plot~ f(x)=1/11*(3x^4-16x^3+24x^2) ; {0|0} ; {1|1} ; {2|16/11} ;[[-1|3,5|-0,5|4]] ~plot~

Comments

An der Stelle x = 2 liegt doch bei diesem Graphen ein Minimum vor oder nicht?

---

Danke dir, Arsinoe4... hatte irgendwie einen Blackout. Habe es korrigiert ;)

---

Ist nun bei x=2 ein Sattelpunkt?

---

Da ist immer noch kein Sattelpunkt zu sehen. Die Steigung an der Stelle x = 2 ist nicht Null.

---

Es muss doch gelten f'(2) = 0 und f''(2) = 0, da waagerechte Tangente (Sattelpunkt)?

---

Hatte irgendwie im Hinterkopf, dass bie \(x=2\) eine Nullstelle sein sollte. Aber diese Forderung existierte nur in meinem Kopf, nicht in der Realität...

---

Hatte irgendwie im Hinterkopf, dass bie \(x=2\) eine Nullstelle sein sollte. Aber diese Forderung existierte nur in meinem Kopf, nicht in der Realität...

.. hast es doch noch gemerkt. Ich hatte den Graphen gerade fertig:$$f\left(x\right)=\frac{1}{11}\left(3x^{4}-16x^{3}+24x^{2}\right)$$

https://www.desmos.com/calculator/c3z7lchb7h

Answer 2

Also du kannst da ein paar Dinge rauslesen:

f(1) = 1

f(0) = 0

f'(2) = 0

f''(2) = 0

Weißt du, wie du nun weiter machen kannst und woher das kommt?

Comments

Eine Bedingung an f fehlt noch.

---

Hmm das stimmt. Sehe aus dem Kontext gerade keine weitere, du?

edit: doch natürlich ("berührt die x-Achse")

d.h. f'(0)=0

---

\(    \)----

---

Ich muss dann diese Eigenschaften in Gleichungen übersetzen

---

Richtig, d.h.:

Erste und zweite Ableitung bilden und Gleichungssystem aufstellen.

Was passiert mit deinem e, siehst du da direkt etwas?

---

Wenn ich mich nicht irre, müsste e= 0 sein

---

Korrekt! Wenn du noch Probleme hast, dann frag hier einfach. Ich oder die anderen helfen dir dann gerne

---

Ich habe mir aufgeschrieben, dass man nach dem ''Übersetzen'' ein Additionsverfahren anwenden muss?

Answer 3

Dank den Vorarbeiten nun der Lösungsweg:

f(1) = 1    f(0) = 0   f´(0)=0    f'(2) = 0    f''(2) = 0

f(x)=a*x^4+b*x^3+c*x^2+d*x+e

f(1)=a+b*+c+d+e

1.) a+b+c+d+e=1

f(0)=e   

2.)e=0

f´(x)=4a*x^3+3b*x^2+2c*x+d

f´(0)=d

3.)d=0

f´(2)=4a*2^3+3b*2^2+2c*2+d=32a+12b+4c

4.)32a+12b+4c=0    8a+3b+c=0

f´´(x)=12a*x^2+6b*x+2c

f´´(2)=12a*2^2+6b*2+2c=48a+12b+2c

5.)48a+12b+2c=0     24a+6b+c=0

a=\( \frac{3}{11} \)    b=-\( \frac{16}{11} \)    c=\( \frac{24}{11} \)

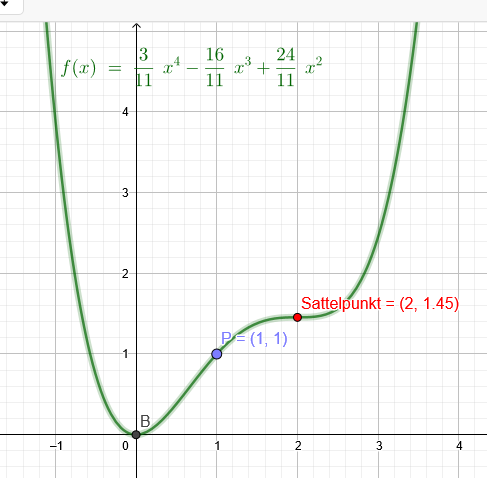
f(x)=\( \frac{3}{11} \) *x^4-\( \frac{16}{11} \)*x^3+\( \frac{24}{11} \)*x^2