Bestimme die Funktionsgleichung f(x) der ganzrationalen Funktion dritten Grades, ...

Question

Aufgabe:

Hallo Leute kann mir einer bitte nur bei a) helfen? Ich komme irgendwie nicht weiter

Problem/Ansatz:

Text erkannt:

Bestimme die Funktionsgleichung \( f(x) \) der ganzrationalen Funktion dritten Grades, ...
a) ... deren Graph den Hochpunkt \( (-1 \mid 16) \) und den Tiefpunkt \( (3 \mid-16) \) besitzt.

Answer 1

Hallo

f(x)=ax^3+bx^2+cx+d

du kennst  f(-1), f(3) f'(-1) und f'(3) hast also 4 einfache Gleichungen für a,b,c,d

Gruß lul

Comments

Danke sehr aber wie soll ich jetzt weiter rechnen wenn ich fragen darf? Bin sehr lost in dieses Thema

---

Hallo

erst mal die Gleichungen alle aufschreiben. di erste ist

-a+b-c+d=16

jetzt du die 3 nächsten, dann die Gleichungen oder Vielfache davon so addieren dass Unbekannte rausfallen .

Gruß lul

Answer 2

Hallo,

stelle aus den beiden Punkten vier Gleichungen auf.

f(x) ist immer der Funktionswert, also y-Koordinate eines Punktes

Bei Extrempunkten gilt immer f'(x) = 0 als notwendige Bedingung

Schreibe zunächst die allgemeine Gleichung einer Funktion dritten Grades und ihrer Ableitung auf:

\( f(a)=a x^{3}+b x^{2}+c x+d \)
\( f^{\prime}(a)=3 a x^{2}+2 b x+c \)

Dann setzt du für den Hochpunkt in die Funktionsgleichung -1 für x und 16 für f(x) ein, anschließend in die Ableitung 0 für f'(x) und -1 für x:

\( f(-1)=16 \Rightarrow-a+b-c+s=16 \)
\( f^{\prime}(-1)=0 \Rightarrow 3 a-2 b+c=0 \)

Das Gleiche machst du für den Tiefpunkt:

\( f(3)=-16 \Rightarrow 27 a+9 b+3 c+d=-16 \)
\( f^{\prime}(3)=0 \Rightarrow 27 a+6 b+c = 0 \)

Nun hast du vier Gleichungen für die vier Variablen.

Gruß, Silvia

Answer 3

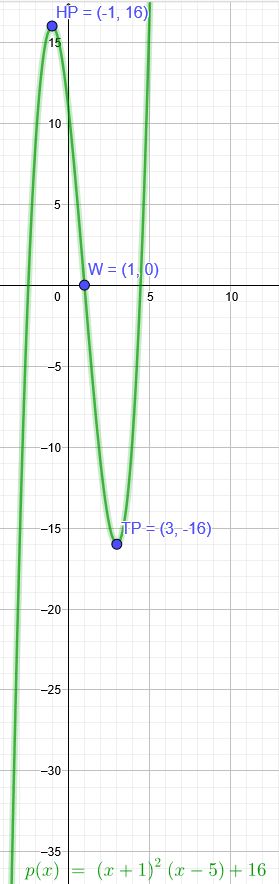
Bestimme die Funktionsgleichung \( f(x) \) der ganzrationalen Funktion dritten Grades, a)  deren Graph den Hochpunkt \( (-1 \mid 16) \) und den Tiefpunkt \( (3 \mid-16) \) besitzt.

Eine Parabel dritten Grades ist immer punktsymmetrisch zum Wendepunkt: \(W(1,0)\)

Ich verschiebe den Graphen um 16 Einheiten nach unten:

Hochpunkt \( H(-1 \mid 16) \)→ Hochpunkt \( H´(-1 \mid 0) \)   → doppelte Nullstelle

Tiefpunkt \( T(3 \mid-16) \) →    Tiefpunkt \( T´(3 \mid-32) \)  

Wendepunkt: \(W(1,0)\)   →  Wendepunkt: \(W´(1,-16)\)

\( f(x)=a*(x+1)^2*(x-N) \)

Tiefpunkt \( T´(3 \mid-32) \):  

\( f(3)=a*(3+1)^2*(3-N)=16a*(3-N)=-32 \)→\(a*(N-3)=2 \)→\(a=\frac{2}{N-3} \)

Wendepunkt: \(W´(1,-16)\)

\( f(1)=\frac{2}{N-3}*(1+1)^2*(1-N)\\=\frac{8}{N-3}*(1-N)=-16 \)

\(\frac{1}{N-3}*(N-1)=2 \)   →  \(N=5 \)   \(a=1 \)

\( f(x)=(x+1)^2*(x-5) \)

Nun wieder um 16 Einheiten nach oben:

\( p(x)=(x+1)^2*(x-5) +16\)