Matherätsel! Hat hier jemand eine Idee?

Question

Aufgabe:

Eine Kanufahrerin befindet sich in einem Gewaesser vor einem geradlinigen Ufer. Die Strecke zum naehesten Punkt A des Ufers beträgt 8 km. Die Kanufahrerin möchte zum kürzestmoeglichen Zeitpunkt den Uferpunkt B erreichen, welcher eine Entfernung von 10 km zu A besitzt. Die Paddelgeschwindigkeit im Wasser betraegt 3 km/h, die Gehgeschwindigkeit an Land 5 km/h. Wie weit liegt der Uferpunkt P, den die Kanufahrerin anzielen muss, vom Punkt A entfernt, damit sie ihr Vorhaben erreicht?

Answer 1

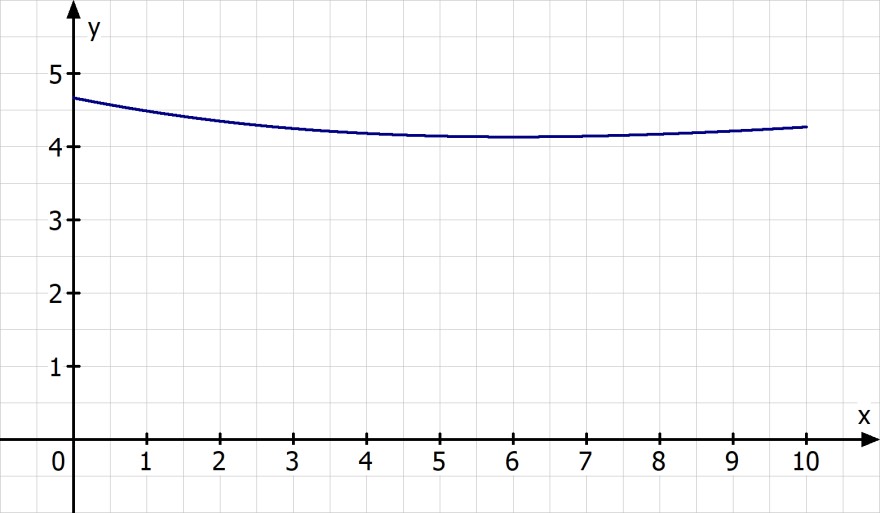
Das wichtigste ist evtl. eine Skizze. Allerdings war die vermutlich eh bei der Aufgabe dabei. Daher hier nur meine grobe Rechnung.

T(x) = √(8^2 + x^2)/3 + (10 - x)/5

T'(x) = x/(3·√(x^2 + 64)) - 1/5 = 0 → x = 6 km

Der Uferpunkt P liegt also 6 km vom Punkt A entfernt.

T(6) = √(8^2 + x^2)/3 + (10 - x)/5 = 4.133 = 4 h 8 min

Sie benötigt also ca. 4 Stunden 8 Minuten

Comments

Zuerst mal danke! Aber verstanden hab ich es jetzt auch noch nicht. Skizze ist keine dabei.

Mir ist zu Beginn schon unklar weshalb sie nicht direkt aus B zusteuern kann, es gibt ja keine Kraft die sie ablenken würde?

vG

---

Sie könnte direkt auf B zusteuern. Allerdings ist das nicht der zeitlich kürzeste Weg.

Wie gesagt ergibt sich der zeitlich kürzeste Weg, wenn P 6km von A entfernt ist. Berechne doch mal für verschiedene Entfernungen von P die benötigte Zeit.

---

Super jetzt hat’s klick gemacht. Danke dir