Brauche Scheitelpunkt über Nullstellen!

Question

Habe gerade eine Aufgabe mit der Formel: y=-2x²+6x-2,5

Die Nullstellen sind x=0,5 v x=3,5

Durch diese Nullstellen muss ich an den Scheitelpunkt kommen!

Wie geht es das?

Answer 1

Achtung: Im folgenden ist ein Fehler, weil sich die Nullstellen nicht wie in der Aufgabe angegeben bei 0,5 und 3,5 befinden! Korrektur weiter unten.

Die x-Koordinate des Scheitelpunktes befindet sich immer genau zwischen den Nullstellen:

Sx = (n₁ + n₂)/2 = (0,5 + 3,5)/2 = 2

Das setzten wir jetzt in die Funktionsgleichung für x ein:

Sy = -2*2^2 + 6*2 - 2,5 = -8 + 12 - 2,5 = 1,5

Der Scheitelpunkt befindet sich also bei S(2 | 1,5)

Comments

Verändert sich dann nicht auch die Funktion?

Die Scheitelpunktform der angebenen Funktion lautet

f(x)=-2(x + 3/2)² +2  setzt man nun den neuen Scheitelpunkt ein?

und erhält dan

f(x) =-2(x-2)²+1,5 ?

---

@Akelei: Du hast bei deiner Scheitelpunktform das – vor der 2 verloren.

---

Ah. Ich verstehe was Akelei meint. Das Problem war, ich habe die gegebenen Nullstellen als bekannt vorausgesetzt. Die Funktion

f(x) = -2x^2 + 6x - 2.5

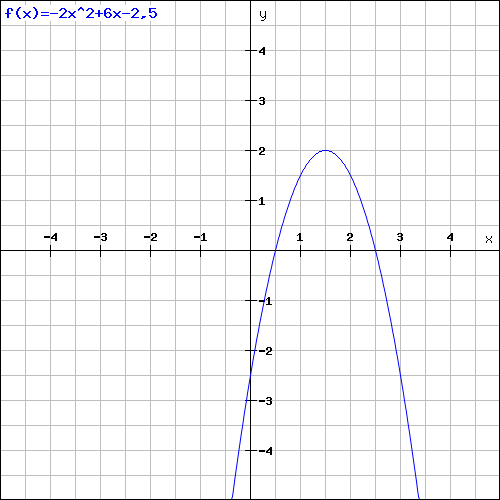
hat aber keine Nullstellen bei 0,5 und 3,5 sondern bei 0,5 und 2,5 !! Damit kommt man zwangweise auf eine verkehrte Sx-Koordinate

Sx = (n₁ + n₂)/2 = (0,5 + 2,5)/2 = 1,5
Sy = -2*(1,5)^2 + 6*1,5 - 2.5 = -4,5 + 9 - 2,5 = 2

Damit liegt der Scheitelpunkt bei S(1,5 | 2).

Damit lautet die Scheitelpunktform der Funktion

f(x) = -2(x - 1,5)^2 + 2

Also Achtung: Die oben gegebenen Nullstellen sind verkehrt !!

Hier noch der Graph der Funktion

---

danke , habe es auch schon  geändert.