a) Durch die GLeichung y = f(x) = x²+2x-2 ist eine Funktion gegeben.
- geben sie ihren WErtebereich an!
Scheitelpunkt ist zwischen den Nullstellen bei -p/2 also bei
x = -p/2 = -2/2 = -1 und
f(-1) = -3
Wertebereich der nach oben geöffneten Parabel ist also W = [-3 ; ∞]
-zeichnen sie den graph dieser funktion mindestens im intervall -4≤x≤2!
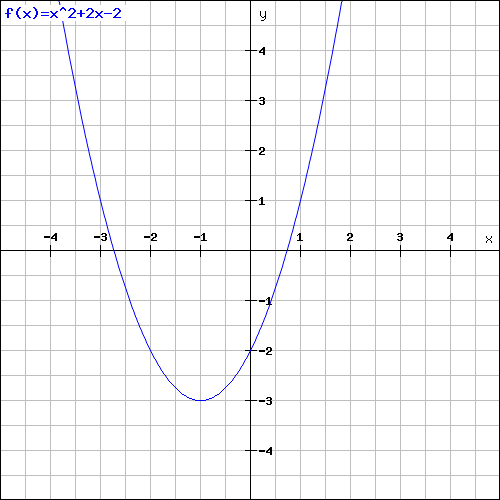
c)
Die graphen scheiden einander in P(xp;yp)
-geben sie die koordinaten von P an!
-überprüfen sie rechnerisch ob das von ihnen angegebene zahlenpaar zu beiden funktionen gehört
Welches ist die andere Funktion ?
und aufgabe 2:
gegeben ist die funktion f durch ihre gleichung y=f(x)=x²-2x-1
a)ermitteln sie die koordinaten des scheitelpunktes und zeichnen sie den graph dieser funktion mindestens im intervall -2≤x≤3 in ein koordinatensystem
Scheitelpunkt ist auch hier wieder
x = -p/2 = 2/2 = 1
f(1) = -2
S(1 | -2)

b)prüfen sie rechnerisch ob x=2,5 eine nullstelle der funktion f ist.
f(2,5) = 2,5²-2*2,5-1 = 0,25 <> 0
2,5 ist also keine Nullstelle
c) zeichnen sie din dasselbe koordinatensystem eine gerade g die den graph der funktion f in genau zwei punkten schneidet und nicht parallel zur xachse verläuft. die gerade g ist das bild einer linearen funktion.
geben sie deren funktionsgleichung an.
g(x) = x
