Hallo Elena,
hier bietet es sich an, zunächst alle Winkel in dem Viereck zu berechnen. Inklusive der Winkel an der Diagonalen \(e\). Dazu folgende Tabelle$$\begin{array}{llr}\alpha& \checkmark& 78.2\\ \beta& \checkmark& 102.5\\ \gamma& \checkmark& 90.0\\ \angle(ae)& \checkmark& 52.1\\ \angle(eb)& =180-\beta-\angle(ae)& 25.4\\ \angle(ed)& =\alpha-\angle(ae)& 26.1\\ \angle(ce)& =\gamma-\angle(eb)& 64.6\\ \delta& =180-\angle(ed)-\angle(ce)& 89.3\end{array}$$Nun kann man die fehlenden Seiten und die Diagonale \(e\) jeweils mit dem Sinussatz berechnen. Im Dreieck \(\triangle ABC\) ist$$e=a\frac{\sin(\beta)}{\sin(\angle(eb))}\approx 495,05$$Die Längen kannst Du der Skizze entnehmen:
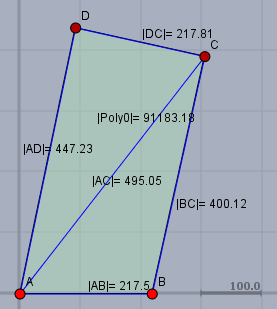
Am einfachsten kommt man nun mit dem Satz von Heron weiter, um die Flächen der Dreieck \(\triangle ABC\) und \(\triangle ACD\) zu berechnen. Die Fläche \(F\) eines Dreicks mit den drei Seiten \(a\), \(b\) und \(c\) berechnet sich nach$$F=\sqrt{s(s-a)(s-b)(s-c)} \quad s=\frac{a+b+c}2$$
Ich habe$$F_{\triangle ABC} \approx 42480\,\text m^2\\ F_{\triangle ACD} \approx 48700\,\text m^2$$macht zusammen ca. \(9,12\,\text{ha}\). Falls etwas unklar ist, so frage bitte nach.
Gruß Werner