Bestimmen Sie alle Punkte x \in[0,1] , in denen f stetig ist.

Question

Aufgabe:

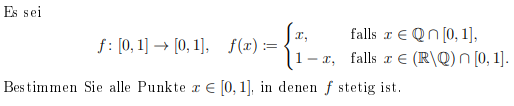
Text erkannt:

Es sei
\( f:[0,1] \rightarrow[0,1], \quad f(x):=\left\{\begin{array}{ll} x, & \text { falls } x \in \mathbb{Q} \cap[0,1] \\ 1-x, & \text { falls } x \in(\mathbb{R} \backslash \mathbb{Q}) \cap[0,1] \end{array}\right. \)
Bestimmen Sie alle Punkte \( x \in[0,1] \), in denen \( f \) stetig ist.

Problem/Ansatz:

Ich hatte die Frage schon hier gesehen, aber leider konnte ich mit der Antwort nicht viel anfangen. Es ist nicht wirklich mein Thema, daher bitte ich um Hilfe.

Answer 1

Hallo

Benutze die Folgenstetigkeit: und jede reelle Zahl kann man durch eine Folge von rationalen Zahlen beliebig annähern, ebenso jede rationale Zahl durch eine Folge nicht rationaler Zahlen.

Gruß lul

Comments

Danke für die Antwort. Aber wenn ich ehrlich bin ist es echt nicht mein Thema und ich verstehe nur Bahnhof. Wäre es möglich eine der Gleichungen zu lösen, damit ich die verstehen kann wie ich sowas angehen muss um auf eine Lösung zu kommen. Ich denke dass würde mir am meisten bringen. Vielen Dank

---

Hallo

Da gibts keine Gleichung!  und "ist es echt nicht mein Thema" hilft ja wenig!

Weisst du was Stetigkeit ist? wie man Stetigkeit mit Folgen zeigt? Da gibts so was wie ne Gleichung; f(x) ist bei x0 stetig wenn für JEDE Folge \( \lim\limits_{n\to\infty} xn=x0\)  gilt ,\( \lim\limits_{n\to\infty} f(xn)=f(x0)\)

Und mach das besser zu deinem Thema! oder was studierst du? ( für Sport oder Jura etwa muss das nicht dein Thema sein)

Gruß lul