Hallo,
ich werde dir Aufgabe a) ohne Rechenwege erklären. Dann kannst du sagen, was du noch nicht verstanden hast. Wenn das geklärt ist, solltest du dich selber an die anderen beiden Aufgaben wagen.
Bilde zunächst die ersten drei Ableitungen der Funktion.
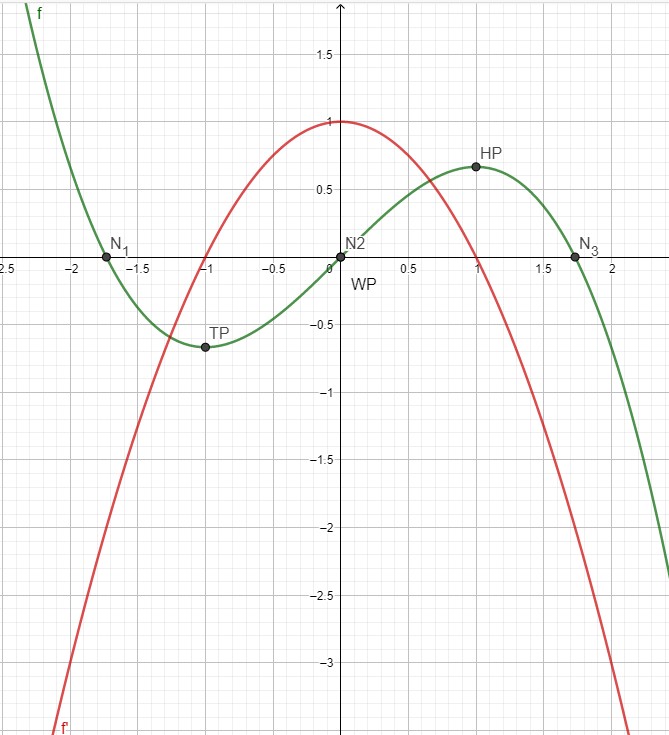
\( f(x)=-\frac{1}{3} x^{3}+x \)
\( f^{\prime}(x)=-x^{2}+1 \)
\( f^{\prime \prime}(x)=-2 x \)
\( f^{\prime \prime\prime}(x)=-2 \)
Schnittpunkte mit der x-Achse = Nullstellen - Setze f(x) = 0 und löse nach x auf.
\( -\frac{1}{3} x^{3}+x=0 \)
\( x_{1}=-1,73 \)
\( x_{2}=0 \)
\( x_{3}=1,73 \)
Schnittpunkt mit der y-Achse: Setze 0 für x in f(x) ein und rechne. x = 0
Hoch- und Tiefpunkte: Setze f'(x) = 0 und löse nach x auf. Setze deine Ergebnisse in f(x) ein, um die y-Koordinaten zu bestimmen. Setze deine Ergebnisse in f''(x) ein, um zu prüfen, ob es sich um einen Hoch- oder Tiefpunkt handelt.
Ist das Ergebnis kleiner null, liegt ein Hochpunkt vor.
Ist das Ergebnis größer null, liegt ein Tiefpunkt vor.
\( -x^{2}+1=0 \)
\( x^{2}=1 \)
\( x_{1/ 2} =\pm 1 \)
\( f(1)=\frac{2}{3}, \;f^{\prime\prime}(1)=-2 \)
\( f(-1)=-\frac{2}{3}, \;f^{\prime \prime}(-1)=2 \)
\( H P\left(1 \mid \frac{2}{3}\right) \)
\( \operatorname{TP}\left(-1 \mid-\frac{2}{3}\right) \)
Wendepunkte: Setze f''(x) = 0 und löse nach x auf, weitere Bedingung \(f'''(x)\neq 0\)
WP (0|0)
Monotoniekriterium
\( f^{\prime}(x)<0 \) im Intervall I \( \Rightarrow \) Der Graph von \( f \) fällt streng monoton in \( I \).
\( f^{\prime}(x)>0 \) im Intervall \( I \Rightarrow \) Der Graph von \( f \) steigt streng monoton in \( I \).
Hier also:
von minus unendlich bis zum Tiefpunkt ist die Funktion streng monoton fallend, vom TP bis HP ist sie streng monoton steigend, nach dem Hochpunkt wieder fallend.
Gruß, Silvia