Hallo,
bilde die ersten beiden Ableitungen der Funktion:
\( f(x)=-x^{3}+6 x^{2} \)
\( f^{\prime}(x)=-3 x^{2}+12 x \)
\( f^{\prime \prime}(x)=-6 x+12 \)
Zur Berechnung der Nullstellen = Schnittpunkte mit der x-Achse setze f(x) = 0 und löse nach x auf.
\( f(x)=0 \)
\( -x^{3}+6 x^{2}=0 \)
\( x^{2} \cdot(-x+6)=0 \)
\( x=0 \quad \vee -x+6=0 \Rightarrow x=6 \)
Also hat die Funktion eine doppelte Nullstelle bei x = 0 und eine weitere bei x = 6.
Schnittpunkt mit der y-Achse: Berechne f(0)
\(f(0)=-0^3+6\cdot 0^2=0\)
Die Funktion schneidet die y-Achse an der Stelle x = 0.
Extrempunkte
Setze die 1. Ableitung = 0 und löse nach x auf:
\(-3x^2+12x=0\\ x\cdot(-3x+12)=0 \\ x = 0\qquad \vee \qquad -3x+12=0\Rightarrow x=4\)
Um festzustellen, ob es sich einen Hoch- bzw. Tiefpunkt handelt, setze die Ergebnisse in die 2. Ableitung ein.
\(f''(0)=-6\cdot 0+12=12\\ 12>0\Rightarrow \text{Tiefpunkt}\\ f''(4)=-12\\ -12<0\Rightarrow \text{Hochpunkt}\)
Jetzt brauchst du noch die y-Koordinaten der Extrempunkte, setze dafür deine Ergebnisse in f(x) ein.
Für das Monotonieverhalten gilt
\( f^{\prime}(x)<0 \) im Intervall I \( \Rightarrow \) Der Graph von \( f \) fällt streng monoton in \( I \).
\( f^{\prime}(x)>0 \) im Intervall I \( \Rightarrow \) Der Graph von \( f \) steigt streng monoton in \( I \).
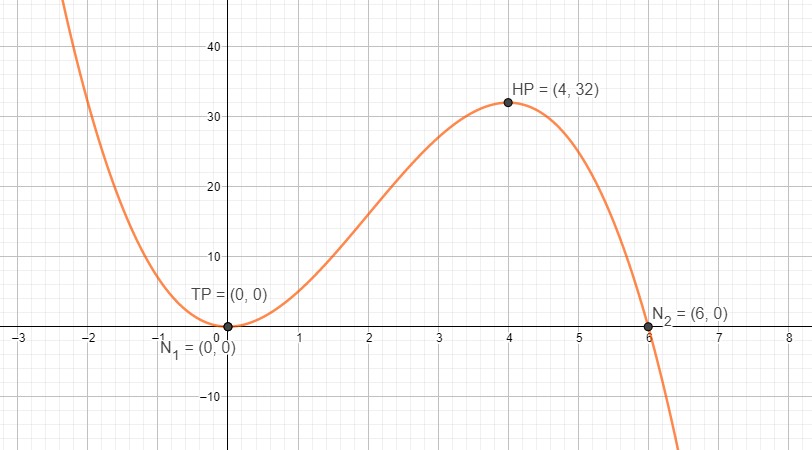
Links vom Tiefpunkt ist die Funktion streng monoton fallend, steigend zwischen Tiefpunkt und Hochpunkt, danach wieder fallend.
 Gruß, Silvia
Gruß, Silvia