Aufgabe:
Stimmt mein Beweis für Teil 2?
Beweis no 1, habe schon gemacht und jetzt NUR noch Beweis no 2
zuerst der Beweis wie im Buch


Text erkannt:
(2) Wenn-dann-Formulierungen von Satzen
Beim Beweis des obigen Satzes aber die gegenüberliegenden Winkel im Sehnenviereck sind wie von einem Sehnenviereck (als Voraussetzung) ausgegangen, bei dem nach Definition alle vier Eckpunkte auf einem Kreis liegen. Daraus haben wir u.a. mithilfe des Basiswinkelsatzes für gleichschenklige Dreiecke und des Innenwinkelsatzes für Vierecke gefolgert, dass gegenüberliegede Winkel zusammen \( 180^{\circ} \) groß sind (Behauptung), Das bringt man deutlicher zum Ausdruck, wenn man den obigen Satz wie folgt formuliert:
Wenn ein Viereck ein Sehnemiereck ist, dann sind gegenüberliegende Innenwinkel zusammen \( 180^{\circ} \) gross.
In der Wenn-dann-Formulierung eines Satzes steht hinter dem .. Wenn" die Voraussetzung und hinter dem . Dann " die Behauptung.
Jeden Satz, der mit für jedes... gilt,... beginnt, kann man mit Wenn .... dann formulieren.
Weiterführende
Aufgaben
2. Vervollständigung der Fallunterscheidung
Beweise den Satz über die Innenwinkel im Sehnenviereck für die Fälle:
(1) M liegt auf einer Viereckseite:
(2). M liegt auBerhalb des Vierecks,
3. Widerlegen einer Vermutung durch ein Gegenbeispiel
Tom betrachtet Rechtecke und behauptet dann:
Wenn in einem Viereck nebeneinanderliegende Innenwinkel zusammen \( 180^{\circ} \) betragen, dann handelt es sich um ein Sehnenviereck.
Widerlege Toms Aussagen.
Problem/Ansatz:
Jetzt kommt die Aufgab no 2, Teil 2--> Mittelpunkt liegt außerhalb von Viereck

Text erkannt:
(2) Wenn-dann-Formulierungen von Satzen
Beim Beweis des obigen Satzes aber die gegenaberliegenden Winkel im Sehnemviereck simd wir von cinem Schnenviereck (als Voraussetzang) ausgegangen, bei dem nach Definition alle vier Eckpunkte auf einem Kreis liegen. Daraus haben wir u.a. mithilfe des Basiswinkelsatzes für gleichschenklige Dreiecke und des Innenwinkelsatzes für Vierecke gefolgert, dass gegenüberliegende Winkel zusammen \( 180^{\circ} \) groß sind (Behauptung), Das bringt man deutlicher zum Ausiruck, wenn man den obigen Satz wie folgt formuliert:
Wenn ein Viereck ein Sehnemiereck ist, dann sind gegeniberlicgende Innenwinkel zusammen \( 180^{\circ} \) grob.
In der Wenn-dann-Formulierung eines Satzes steht hinter dem .. Wenn" die Voraussetzung und hinter dem . Dann " die Beltauptung.
Jeden Satz, der mit Fir jedes... gilf,... beginnt, kann man mit Wenn .... dann formulieren.
Weiterführende-
2. Vervollständigung der Fallunterscheidtug
Aufgaben
Beweise den Satz uber die Innenwinkel im Sehnerviereck für die Falle:
(1) M liegt auf einer Viereckseite:
(2). M liegt auBerhalb des Vierecks,
3. Widerlegen einer Vermatung durch ein Gegenbeispiel
- Tom betrachtet Rechtecke und behauptet dana:
Wenn in einem Viereck nebeneinanderliegende Innenwinkel zusammen \( 180^{\circ} \) betragen, dann handeli es sich um ein Sehnenviereck.
Widerlege Toms Aussagen.
…
BIld für den zweiten Beweis
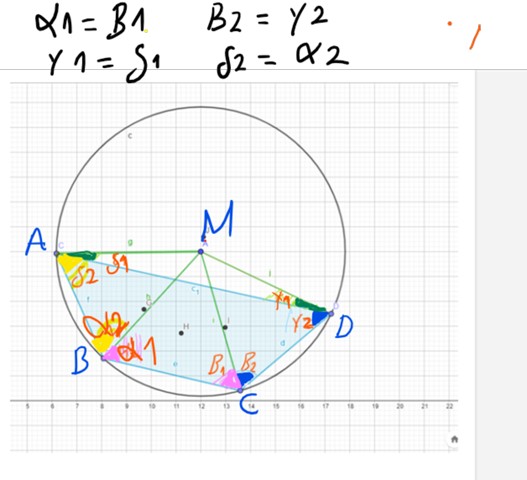
Text erkannt:
\( \begin{array}{ll}\alpha_{1}=B_{1} & B_{2}=y_{2} \\ y_{1}=\delta_{1} & \delta_{2}=\alpha_{2}\end{array} \)
Jetzt Beweis( stimmt)?

Text erkannt:
Bchayphing
\( \alpha_{a} y \) und \( B+S=180 \)
zum Betres verbinden wir dis Miltelpoultt des comicreses mH den 4 ECKpancten \( A, B, C, D \)
Dreiceke \( \triangle B M^{\circ} ; B C M ; C D M \) sind gerchschenklig, denn \( \overline{M A} ; \overline{M B}, \overline{M C}, \overline{M D} \)
Diese sind Basis ven glachionlises breiedle.
Durch zerlegen des schenshereks sind an den Eacpunkten ingesamt 8 winkel. Farbt man glach groze winkel \( m \) " derselben Farber, so benirigt man ver Farben. Writ er kennar num inden zuri gegirivberlizgenden hinkel \( \alpha \) and \( y \) kommen alle vie farben
alpha 1 = Betta 1
Betta 2= Gamma1 + Gamma2
Alph2 = Deöta 1 + Delta 2

Text erkannt:
Bchayphing
\( \alpha_{a} y \) und \( B+S=180 \)
zum Betres verbinden wir dis Miltelpoultt des comicreses mH den 4 ECKpancten \( A, B, C, D \)
Dreiceke \( \triangle B M^{\circ} ; B C M ; C D M \) sind glechschenklig, denn \( \overline{M A} ; \overline{M B}, \overline{M C}, \overline{M D} \)
Diese sind Basis ven glachionlises breiedle.
Durch zerlegen des schenshereks sind an den Eacpunkten ingesamt 8 winkel. Farbt man glach groze winkel \( m \) " derselben Farber, so benirigt man ver Farben. Writ er kennar num inden zuri gegirivberlizgenden hinkel \( \alpha \) and \( y \) kommen alle vie farben

Text erkannt:
Farben, so benurigt man ver Farben. Wort ben Crinkel \( \alpha \) cund Winkel \( \alpha \) and \( y \) kommen alle vie ferben gelb; lila, grün, blau ebenso, in \( > \) dengegenliberlizgenden vinkel \( B \) unds.
\( \alpha+y=\beta+\delta \)
\( \alpha+y=\alpha_{1}+\left(\alpha_{2}\right)+\left(y_{1}+y_{2}\right) \)
weilar obongezeyt dass \( \rightarrow \alpha_{1}=B A \)
\( \left.=B_{1}+\left(S^{2}+\int \limits_{1}\right)+P_{2}\right) \quad B^{2}=13^{2} \times 1=2 \) \( =\left(B_{1}+B_{2}\right)+\left(S_{1}+S_{2}\right) \)
wenn minkelsume in vierck 360 . damn de zwei gegon uber liegenden uink \( 180 \Rightarrow \alpha+y=180 \quad B+\delta=180 \)